Преобразование Фурье

Преобразование Фурье – это семейство математических методов, основанных на разложении исходной непрерывной функции от времени на совокупность базисных гармонических функций (в качестве которых выступают синусоидальные функции) различной частоты, амплитуды и фазы. Из определения видно, что основная идея преобразования заключается в том, что любую функцию можно представить в виде бесконечной суммы синусоид, каждая из которых будет характеризоваться своей амплитудой, частотой и начальной фазой.

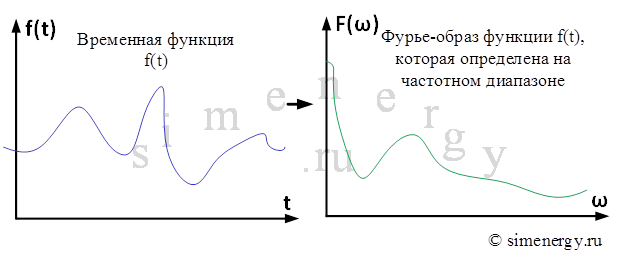
Рис. 1. Функция, которая определена на временном интервале, и ее отображение на частотном интервале

 Преобразование Фурье является основоположником спектрального анализа. Спектральный анализ – это способ обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. В зависимости от того, каким образом представлен сигнал, используют разные преобразования Фурье. Различают несколько видов преобразования Фурье:

– Непрерывное преобразование Фурье (в англоязычной литературе Continue Time Fourier Transform – CTFT или, сокращенно, FT);

– Дискретное преобразование Фурье (в англоязычной литературе Discrete Fourier Transform – DFT);

– Быстрое преобразование Фурье (в англоязычной литературе Fast Fourier transform – FFT).

Непрерывное преобразование Фурье

Преобразование Фурье является математическим инструментом, применяемым в различных научных областях. В некоторых случаях его можно использовать как средство решения сложных уравнений, описывающих динамические процессы, которые возникают под воздействием электрической, тепловой или световой энергии. В других случаях оно позволяет выделять регулярные составляющие в сложном колебательном сигнале, благодаря чему можно правильно интерпретировать экспериментальные наблюдения в астрономии, медицине и химии. Непрерывное преобразование фактически является обобщением рядов Фурье при условии, что период разлагаемой функции устремить к бесконечности. Таким образом, классическое преобразование Фурье имеет дело со спектром сигнала, взятым во всем диапазоне существования переменной.

Существует несколько видов записи непрерывного преобразования Фурье, отличающихся друг от друга значением коэффициента перед интегралом (две формы записи):

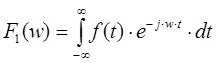 или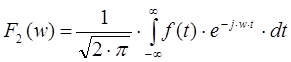 

где  и - Фурье-образ функцииили частотный спектр функции ;

 - круговая частота.

Следует отметить, что разные виды записи встречаются в различных областях науки и техники. Нормировочный коэффициент необходим для корректного масштабирования сигнала из частотной области во временную. Нормировочный коэффициент уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала. В математической литературе прямое и обратное преобразование Фурье умножаются на множитель , в то время как в физике чаще всего при прямом преобразовании множитель не ставят, а при обратном ставят множитель . Если последовательно рассчитать прямое преобразование Фурье некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом.

• Если функция нечетная на интервале (−∞, +∞), то преобразование Фурье может быть представлено через синус-функцию:

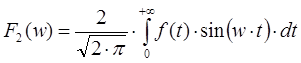
• Если функция четная на интервале (−∞, +∞), то преобразование Фурье может быть представлено через косинус-функцию:

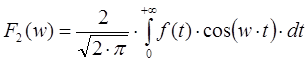
Таким образом, непрерывное преобразование Фурье позволяет представить непериодическую функцию в виде интеграла функции, представляющей в каждой своей точке коэффициент ряда Фурье для непериодической функции.

Преобразование Фурье является обратимым, то есть если по функции  был рассчитан ее Фурье-образ , то по Фурье-образу можно однозначно восстановить исходную функцию . Под обратным преобразованием Фурье понимают интеграл вида (две формы записи):

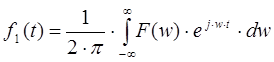 или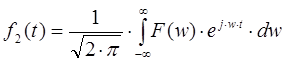 

где  - Фурье-образ функцииили частотный спектр функции ;

 - круговая частота.

• Если функция нечетная на интервале (−∞, +∞), то обратное преобразование Фурье может быть представлено через синус-функцию:

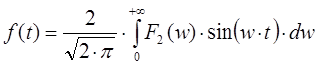
• Если функция четная на интервале (−∞, +∞), то обратное преобразование Фурье может быть представлено через косинус-функцию:

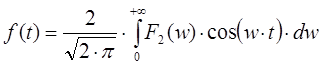
В качестве примера, рассмотрим следующую функцию . График исследуемой экспоненциальной функции представлен ниже.

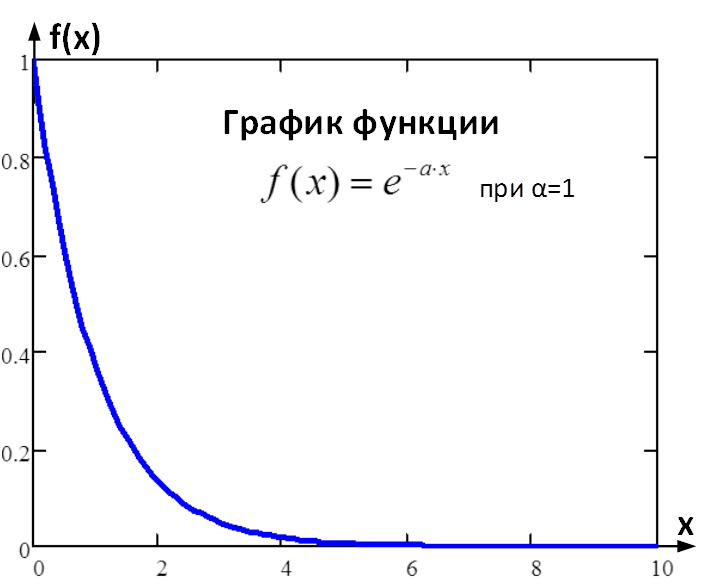
Рис. 2. График исследуемой экспоненциальной функции

Поскольку функция  является четной функцией, то непрерывное преобразование Фурье будет определяться следующим образом:

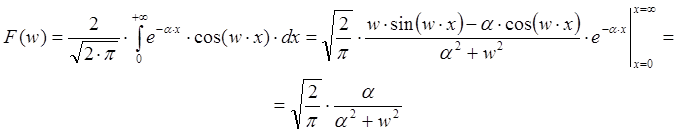
В результате получили зависимость изменения исследуемой экспоненциальной функции на частотном интервале (см. ниже).

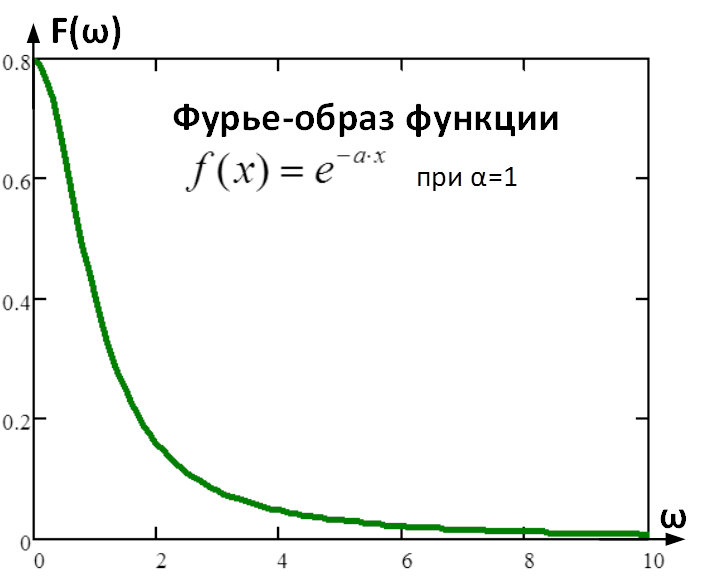
Рис. 3. Фурье-образ исследуемой экспоненциальной функции

Дискретное преобразование Фурье

Непрерывное преобразование Фурье используют, как правило, в теории при рассмотрении сигналов, которые изменяются в соответствии с заданными функциями, но на практике обычно имеют дело с результатами измерений, которые представляют собой дискретные данные. Результаты измерений фиксируются через равные промежутки времени с определённой частотой дискретизации, например, 16000 Гц или 22000 Гц. Однако в общем случае дискретные отсчёты могут идти неравномерно, но это усложняет математический аппарат анализа, поэтому на практике обычно не применяется.

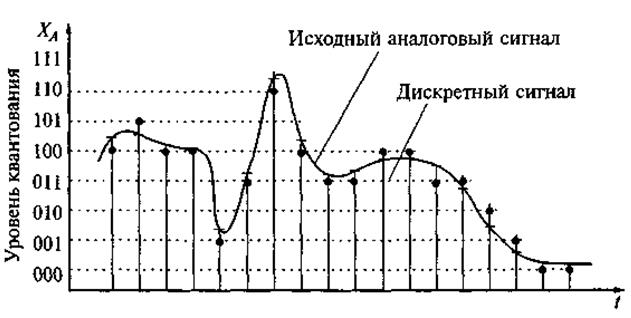
Рис. 4. Исходный аналоговый сигнал и дискретный сигнал

Существует важная теорема Котельникова (в иностранной литературе встречается название «теорема Найквиста-Шеннона», «теорема отсчетов»), которая гласит, что аналоговый периодический сигнал, имеющий конечный (ограниченный по ширине) спектр (0…fmax), может быть однозначно восстановлен без искажений и потерь по своим дискретным отсчётам, взятым с частотой, большей или равной удвоенной верхней частоте спектра -  частота дискретизации (fдискр >= 2*fmax). Другими словами, при частоте дискретизации 1000 Гц из аналогового периодического сигнала можно восстановить сигнал с частотой до 500 Гц. Следует отметить, что дискретизация функции по времени приводит к периодизации ее спектра, а дискретизация спектра по частоте приводит к периодизации функции.

Дискретное преобразование Фурье  — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов.

• Прямое дискретное преобразование Фурье ставит в соответствие временной функции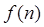, которая определенаN-точками измерений на заданном временном интервале, другую функцию 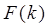, которая определена на частотном интервале. Следует отметить, что функция на временном интервале задается с помощью N-отсчетов, а функция на частотном интервале задается с помощью K-кратного спектра.

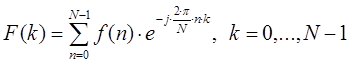
N ˗ количество значений сигнала, измеренных за период, а также кратность частотного спектра;

k ˗ индекс частоты.

Частота k-го сигнала определяется по выражению

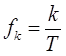
где T — период времени, в течение которого брались входные данные.

Прямое дискретное преобразование может быть переписано через вещественную и мнимую составляющие. Вещественная составляющая представляет собой массив, содержащий значения косинусоидальных составляющих, а мнимая составляющая представляет собой массив, содержащий значения синусоидальных составляющих.

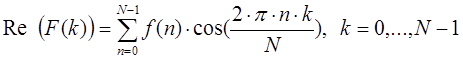
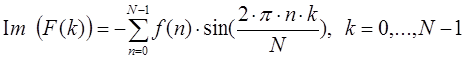
Из последних выражений видно, что преобразование раскладывает сигнал на синусоидальные составляющие (которые называются гармониками) с частотами от одного колебания за период до N колебаний за период.

Дискретное преобразование Фурье имеет особенность, так как дискретная последовательность может быть получена суммой функций с различным составом гармонического сигнала. Другими словами,   дискретная последовательность раскладывается на гармонические переменные – неоднозначно. Поэтому при разложении дискретной функции с помощью дискретного преобразования Фурье во второй половине спектра возникают высокочастотные составляющие, которых не было в оригинальном сигнале. Данный высокочастотный спектр является зеркальным отображением первой части спектра (в части частоты, фазы и амплитуды). Обычно вторая половина спектра не рассматривается, а амплитуды сигнала первой части спектра - удваиваются.

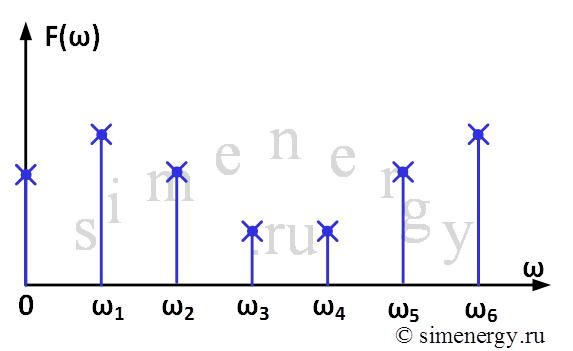
Рис. 5. «Зеркальный эффект» на спектре частоты для дискретного сигнала

Следует отметить, что разложение непрерывной функции не приводит к появлению зеркального эффекта, так как непрерывная функция однозначно раскладывается на гармонические переменные.

Амплитуда постоянной составляющей является средним значением функции за выбранный промежуток времени и определяется следующим образом:

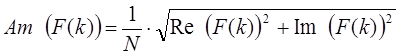
Амплитуды и фазы частотных составляющих сигнала определяются по следующим соотношениям:

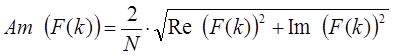
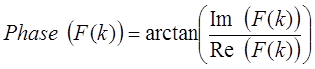
Полученные значения амплитуды и фазы называют полярным представлением (polar notation). Результирующий вектор сигнала будет определяться следующим образом:

Рассмотрим алгоритм преобразования дискретно заданной функции   на заданном интервале (на заданном периоде) с количеством исходных точек 

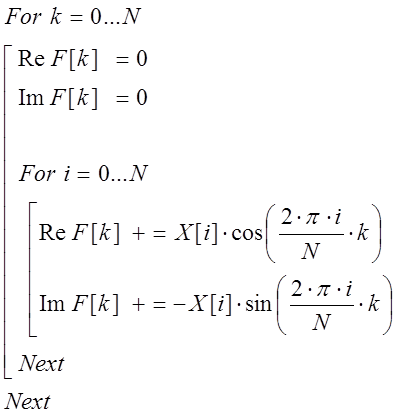
Рис. 6. Дискретное преобразование Фурье

В результате преобразования получаем вещественное и мнимое значение функции , которая определена на частотном диапазоне.

• Обратное дискретное преобразование Фурье ставит в соответствие частотной функции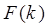, которая определенаK-кратным спектром на частотном интервале, другую функцию 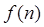, которая определена на временном интервале.

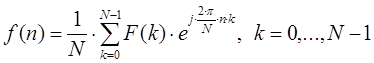
N ˗ количество значений сигнала, измеренных за период, а также кратность частотного спектра;

k ˗ индекс частоты.

Как уже было сказано, дискретное преобразование Фурье N-точкам дискретного сигнала  ставит в соответствие N-комплексных спектральных отсчетов сигнала . Для вычисления одного спектрального отсчета требуется N операций комплексного умножения и сложения. Таким образом, вычислительная сложность алгоритма  дискретного преобразования Фурье является квадратичной, другими словами требуется  операций комплексного умножения и сложения.

Быстрое преобразование Фурье

Быстрое преобразование Фурье (БПФ, Fast Fourier transform - FFT) представляет собой определенный алгоритм вычисления, который позволяет уменьшить количество производимых действий относительно прямого (по формуле) вычисления ДПФ. В основе алгоритма заложено разбиение заданной последовательности отсчетов дискретного сигнала на несколько промежуточных последовательностей. Следует отметить, что алгоритм БПФ точнее стандартного ДПФ, т.к. при сокращении операций снижаются суммарные ошибки округления.

В настоящее время известны несколько алгоритмов быстрого преобразования Фурье, которые являются частными случаями единого алгоритма, базирующегося на задаче разбиения одного массива чисел на два с последующим рекурсивном вычислении каждого массива чисел по дискретному преобразованию Фурье и объединении результатов расчетов.

Рассмотрим алгоритм БПФ с прореживанием по времени. В качестве исходных данных задан N-отсчетный сигнал . Исходный сигнал разбиваем на два массива чисел с -отсчетов: четные отсчеты  и нечетные отсчеты . В результате функция , которая определяется на частотном интервале, будет определяться следующим соотношением:

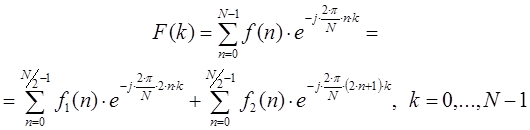
Последнее выражение можно преобразовать в следующий вид:

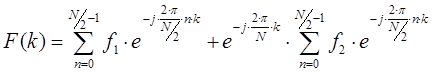
В результате можно получить два выражения для определения функции на первом частотном интервале  и втором частотном интервале :

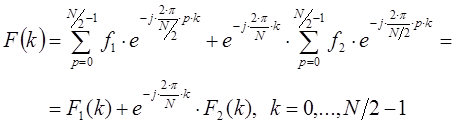
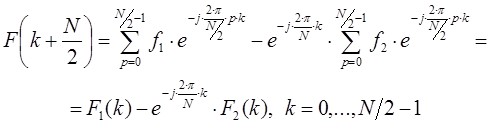
Последнее выражение получено в соответствии со следующими двумя выражениями:

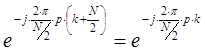
Таким образом, алгоритм вычисления заключается в разбиении входного сигнала  на два массива чисел  и , составленных соответственно из четных и нечетных отсчетов. После этого для каждого массива чисел рассчитывается ДПФ с образованием двух функций   и . На заключительном шаге выполняются базовые операции сложения и вычитания с умножением одного из компонентов на экспоненциальный множитель 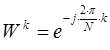. В результате выполнения данных операций получаем функцию . Граф алгоритма БПФ с прореживанием по времени представлен ниже.

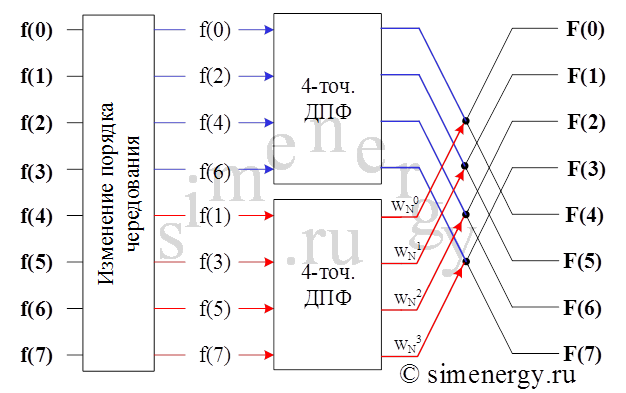
Рис. 7. Граф алгоритма БПФ с прореживанием по времени при делении исходного сигнала на четные и нечетные отсчеты

Из полученного графа видно, что при делении исходного сигнала пополам для вычисления функции , которая определена на частотном интервале, требуется около  комплексных умножений, т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, вычисляя вместо  - отсчетного ДПФ два  - отсчетных ДПФ и сокращая объем вычислений приблизительно в два раза. Эту рекурсию можно продолжать, пока возможно разбить входную последовательность на две.

На структурной схеме  базовую операцию сложения и вычитания с умножением одного из компонентов на экспоненциальный множитель 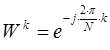 принято показывать сигнальным графом, который в цифровой технике называется  «бабочкой».

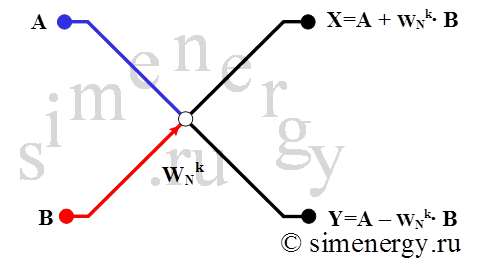
Рис. 8. Операция «бабочка», используемая при реализации алгоритма БПФ

Сигнальный граф показывает каким образом два входных числа А и В объединяются для получения двух выходных чисел X и Y. Изображенный на графе множитель  со стрелкой обозначает один из двух компонентов, который умножается на экспоненциальный множитель.

Рассмотрим алгоритм БПФ с прореживанием по частоте. В качестве исходных данных задан N-отсчетный сигнал . Исходный сигнал разобьём пополам на два массива чисел с  - отсчетными сигналами.

В результате функция , которая определяется на частотном интервале, будет определяться следующим соотношением:

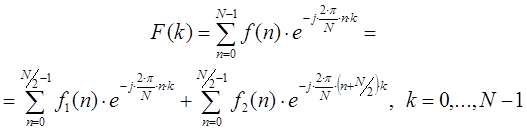
Последнее выражение можно преобразовать в следующий вид:

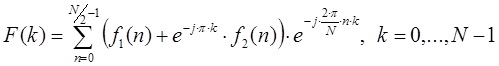
В результате можно записать два выражения для четных и нечетных отсчетов:

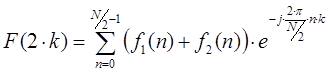
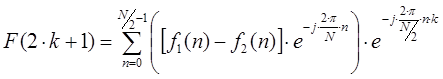
Таким образом, алгоритм вычисления заключается в разбиении входного сигнала  пополам с образованием двух массивов чисел  и . После этого выполняются базовые операции сложения и вычитания с умножением двух компонентов на экспоненциальный множитель 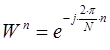. На заключительном шаге рассчитывается ДПФ для четных и нечетных отсчетов с объединением результатов расчета. Граф алгоритма БПФ с прореживанием по частоте представлен ниже.

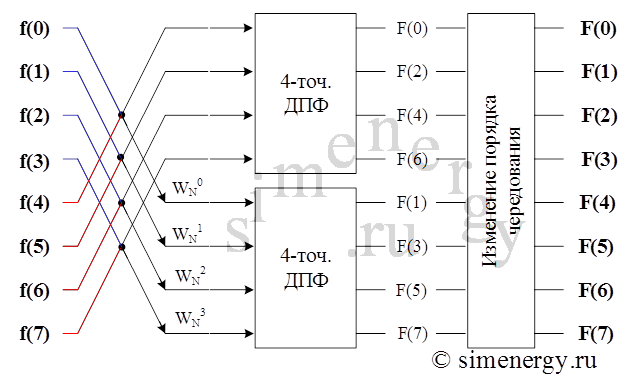
Рис. 9. Граф алгоритма БПФ с прореживанием по частоте при делении исходного сигнала пополам

Из полученного графа видно, что при делении исходного сигнала пополам для вычисления функции , которая определена на частотном интервале, требуется около  комплексных умножений, т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, представляя вместо  - отсчетного ДПФ два  - отсчетных ДПФ и сокращая объем вычислений приблизительно в два раза. Эту рекурсию можно продолжать, пока возможно разбить входную последовательность на две.

Основное отличие рассмотренных алгоритмов быстрого преобразования Фурье заключается в последовательности выполнения базовой операции: в алгоритме БПФ с прореживанием по времени комплексное умножение выполняется перед операцией вычитания,  а в алгоритме БПФ с прореживанием по частоте комплексное умножение выполняется после операции вычитания. Рассмотренные алгоритмы быстрого преобразования Фурье получили наибольшее распространение из-за их высокой эффективности и относительной простоты программной реализации.

В обоих рассмотренных алгоритмах быстрого преобразования Фурье для вычисления функции , которая определена на частотном интервале, из заданного дискретного сигнала с N-количеством значений требуется выполнить  операций комплексного умножения, сложения и вычистания.