Метод Ньютона – это итерационный численный метод (второго порядка) решения оптимизационных задач, который позволяет определить экстремум (минимум или максимум) целевой функции:
- это значения аргумента функции (управляемые параметры), которые определены на вещественной области.
При поиске экстремума целевой функции используется информация о функции и её производных: первого и второго порядка. Итерационная формула для вычисления аргумента функции по методу Ньютона получается при квадратичной аппроксимации целевой функции, т. е. при разложении функции в ряд Тейлора (с отбрасыванием членов третьего и более высоких порядков).
где 
- матрица Гессе, которая представляет собой симметричную квадратную матрицу вторых частных производных целевой функции в точке 
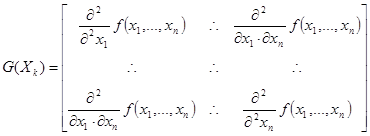
Необходимым условием экстремума функции многих переменных 
в точке является равенство нулю ее производной (градиента) в этой точке:
Продифференцируем функцию, разложенную в ряд Тейлора, по компоненте 
Таким образом, целевая функция имеет экстремум функции при следующем значении ее аргумента:
В общем случае процесс нахождения экстремума функции является итерационной процедурой, поэтому выражение преобразуют к следующему виду:
- вектор столбец управляемых параметров, которые определяются в задаче оптимизации (размерность: 1xn)
- квадратная матрица вторых частных производных (размерность: nxn)
- вектор столбец градиента целевой функции по управляемым параметрам (размерность: 1xn).
Итерационный процесс расчета продолжается до тех пор, пока не будут выполнены некоторые критерии останова:
- траектория поиска остается в малой окрестности текущей точки поиска:
- приращение целевой функции не меняется:
- градиент целевой функции в точке локального минимума обращается в нуль:
Метод Ньютона обладает квадратичной скоростью сходимости, в отличие от других методов первого порядка (Градиентные методы), которые обладают линейной скоростью сходимости. Применение метода Ньютона оказывается очень эффективным при условии, что выполняются необходимые и достаточные условия его сходимости. Условием, гарантирующим сходимость метода Ньютона в предположении, что функция дважды дифференцируема, заключается в том, что матрица Гессе должна быть положительно определенной.
В аналитической геометрии поверхности второго порядка описываются как: эллиптический параболоид, гиперболоид, гиперболический параболоид (седло) и эллипсоид. В задачах поиска минимума квадратичной функции с положительной матрицей вторых производных метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки.
Рис.1. Поиск минимума квадратичной функции по методу Ньютона
При увеличении количества переменных и усложнением функции возникают сложности с вычислением матрицы Гессе, поэтому в настоящее время разработаны квазиньютоновские алгоритмы, основанные на приближённых выражениях для матрицы Гессе. Тем не менее, многие компьютерные программы, решающие задачу оптимизации, построены на основе метода Ньютона. Роль метода Ньютона велика: большинство наиболее эффективных методов в линейном и нелинейном программировании строятся на его основе.
Методика расчета
- 1шаг: Определяем аналитические выражения (в символьном виде) для вычисления градиента рассматриваемой функции и квадратной матрицы Гессе:
градиент рассматриваемой функции:
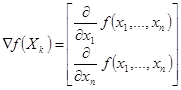
квадратная матрица Гессе:
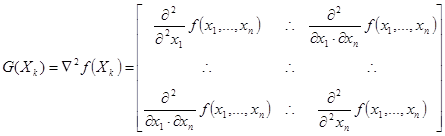
- 2шаг: Задаем начальное приближение
Далее выполняется итерационный процесс.
- 3 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета методомпо следующей формуле:
- 4 шаг:проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
