Метод наискорейшего спуска (в англ. литературе «method of steepest descent») - это итерационный численный метод (первого порядка) решения оптимизационных задач, который позволяет определить экстремум (минимум или максимум) целевой функции:
- это значения аргумента функции (управляемые параметры) на вещественной области.
В соответствии с рассматриваемым методом экстремум (максимум или минимум) целевой функции определяют в направлении наиболее быстрого возрастания (убывания) функции, т.е. в направлении градиента (антиградиента) функции. Градиентом функции в точке называется вектор, проекциями которого на координатные оси являются частные производные функции по координатам:
где i, j,…, n - единичные векторы, параллельные координатным осям.
Градиент в базовой точке 
строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиент), соответственно, показывает направление наискорейшего убывания функции.
Метод наискорейшего спуска является дальнейшим развитием метода градиентного спуска. В общем случае процесс нахождения экстремума функции является итерационной процедурой, которая записывается следующим образом:
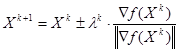
где знак «+» используется для поиска максимума функции, а знак «-» используется для поиска минимума функции;
- единичный вектор направления, который определяется по формуле:
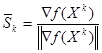
- модуль градиента определяет скорость возрастания или убывания функции в направлении градиента или антиградиента:
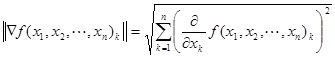
- константа, определяющая размеры шага и одинаковая для всех i-х направлений.
Величина шага выбирается из условия минимума целевой функции f(х) в направлении движения, т. е. в результате решения задачи одномерной оптимизации в направлении градиента или антиградиента:
Другими словами, величину шага 
определяют при решении данного уравнения:
Таким образом, шаг расчета выбирается такой величины, что движение выполняется до тех пор, пока происходит улучшение функции, достигая, таким образом, экстремума в некоторой точке. В этой точке вновь определяют направление поиска (с помощью градиента) и ищут новую точку оптимума целевой функции и т.д. Таким образом, в данном методе поиск происходит более крупными шагами, и градиент функции вычисляется в меньшем числе точек.
В случае функции двух переменных данный метод имеет следующую геометрическую интерпретацию: направление движения из точки 
касается линии уровня в точке 
. Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу. Условие ортогональности векторов направлений спуска в соседних точках записывается следующим выражением:
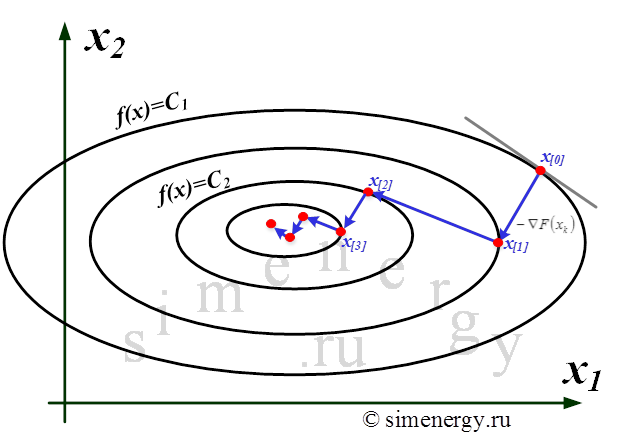
Рис.1. Траектория движения к точке экстремума при использовании метода наискорейшего спуска, изображенная на графике линии равного уровня функции f(x)
Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета (несколько критериев):
- траектория поиска остается в малой окрестности текущей точки поиска:
- приращение целевой функции не меняется:
- градиент целевой функции в точке локального минимума обращается в нуль:
Следует отметить, что метод градиентного спуска оказывается очень медленным при движении по оврагу, причём при увеличении числа переменных целевой функции такое поведение метода становится типичным. Овраг представляет собой впадину, линии уровня которой приближенно имеют форму эллипсов с различающимися во много раз полуосями. При наличии оврага траектория спуска имеет вид зигзагообразной линии с малым шагом, вследствие чего результирующая скорость спуска к минимуму сильно замедляется. Это объясняется тем, что направление антиградиента этих функций существенно отклоняется от направления в точку минимума, что приводит к дополнительной задержке в расчете. В результате алгоритм теряет вычислительную эффективность.
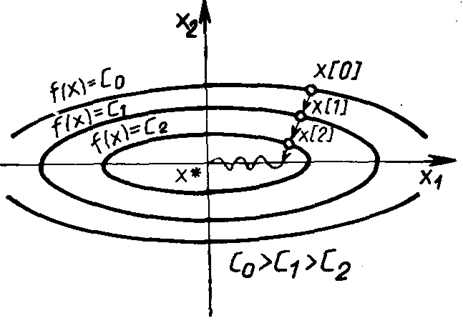
Рис.2. Овражная функция
Метод градиента вместе с его многочисленными модификациями является распространенным и эффективным методом поиска оптимума исследуемых объектов. Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции. Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек. Так же скорость сходимости градиентных методов существенно зависит также от точности вычислений градиента. Потеря точности, а это обычно происходит в окрестности точек минимума или в овражной ситуации, может вообще нарушить сходимость процесса градиентного спуска.
Методика расчета
- 1 шаг:Определение аналитические выражения (в символьном виде) для вычисления градиента функции
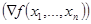
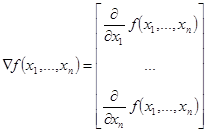
- 2 шаг: Задаем начальное приближение
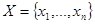
Далее выполняется итерационный процесс.
- 3 шаг:Определяется необходимость рестарта алгоритмической процедуры для обнуления последнего направления поиска. В результате рестарта поиск осуществляется заново в направлении скорейшего спуска.
- 4 шаг: Вычисление координат единичного вектора
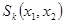по представленным формулам
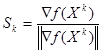
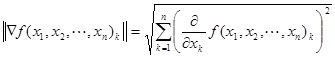
- 5 шаг: определяем шаг расчета из условия поиска экстремума для следующей функции
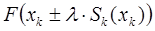(решения задачи одномерной оптимизации).
- 6 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета:
где знак «+» используется для поиска максимума функции, а знак «-» используется для поиска минимума функции;
- 7 шаг:проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
