Выборка экспериментальных данных представляет собой массив данных, который характеризует процесс изменения измеряемого сигнала в течение заданного времени (либо относительно другой переменной). Для выполнения теоретического анализа измеряемого сигнала необходимо найти аппроксимирующую функцию, которая свяжет дискретный набор экспериментальных данных с непрерывной функцией - интерполяционным полиномом n-степени. Одним из способов представления данного интерполяционного полинома n-степени может быть использован многочлен в форме Лагранжа.
Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.
1. Интерполяционная формула Лагранжа
В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде:
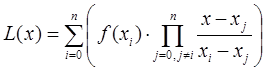
где 
˗ степень полинома 
;
˗ значение значения интерполирующей функции 
в точке 
;
˗ базисные полиномы (множитель Лагранжа), которые определяются по формуле:
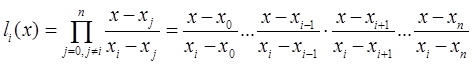
Так, например, интерполяционный многочлен в форме Лагранжа, проходящий через три заданных точки 
, будет записываться в следующем виде:
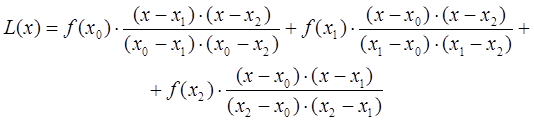
Многочлен в форме Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально 
и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что при построении полинома степени n+1 полностью теряется информация о предыдущем полиноме степени n, т.е. с изменением числа узлов приходится все вычисление выполнить заново.
2. Погрешность интерполяционного полинома в форме Лагранжа
Рассмотрим функцию f(x), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином L(x) в форме Лагранжа принимает в точках 
заданные значения функции 
. В остальных точках интерполяционный полином L(x) отличается от значения функции f(x) на величину остаточного члена, который определяет абсолютную погрешность интерполяционной формулы Лагранжа:
Абсолютную погрешность интерполяционной формулы Лагранжа определяют следующим образом:
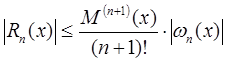
где n ˗ степень полинома 
Переменная 
представляет собой верхнюю границу значения модуля (n +1)-й производной функции f(x) на заданном интервале [a, b]
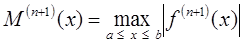
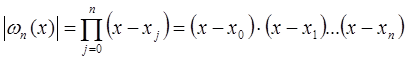
Погрешность интерполяции методом Лагранжа зависит от свойств функции f(x), а также от расположения узлов интерполяции и точки x. В случае если погрешность не достигает нужной точности, то нужно разбить отрезок на части и интерполировать каждую часть в отдельности – кусочная интерполяция.
Выбор узлов интерполяции
С помощью корректного выбора узлов можно минимизировать значение 
в оценке погрешности, тем самым повысить точность интерполяции. Данная задача может быть решена с помощью многочлена Чебышева:
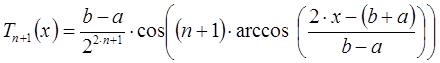
В качестве узлов следует взять корни этого многочлена, то есть точки:
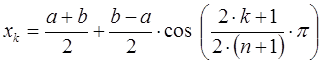
3. Методика вычисления полинома в форме Лагранжа
Алгоритм вычисления полинома в форме Лагранжа позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента:
1. В качестве исходных данных задается выборка из n-точек, которая включает в себя значения функции и значения аргумента функции.
2. Выполняется вычисление полинома n-степени в форме Лагранжа по следующей формуле:
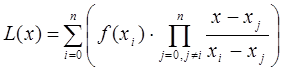
Алгоритм вычисления полинома в форме Лагранжа 
представлен на рисунке 1.
Методика вычисления полинома в форме Лагранжа
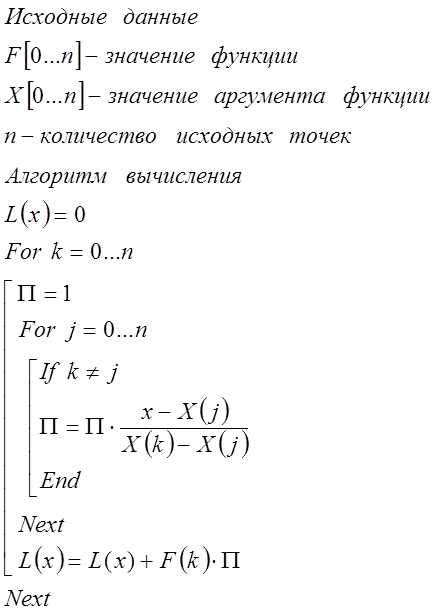
Рис.1. Методика вычисления полинома в форме Лагранжа
В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция 
на интервале [0, 10]. Необходимо построить многочлен в форме Лагранжа для представленного набора значений. С помощью интерполяционной формулы вычислить приближенное значение функции в точке 
, а также определить оценку погрешности результата вычислений.
Многочлен в форме Лагранжа, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Лагранжа показан в графическом виде.
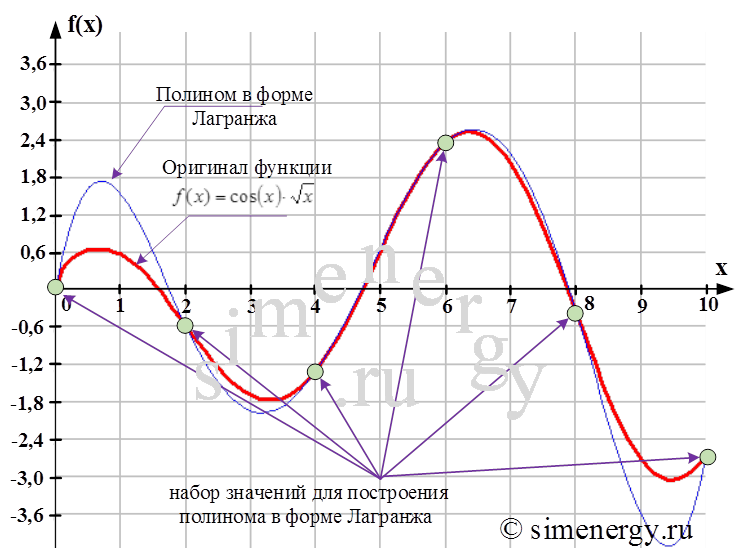
Рис.2. Исходная функция и полином в форме Лагранжа, построенный по шести заданным точкам
С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». В соответствии с условиями задачи полином в форме Лагранжа в точке x=9,5 принимает следующее значение: L(9,5)= – 4,121. Из графика видно, что полученное значение не совпадает cо значением функции f(x) на величину абсолютной погрешности интерполяционной формулы Лагранжа.
Интерполяционный полином в форме Лагранжа часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Лагранжа используются для интерполяции, а также для численного интегрирования таблично-заданной функцией.
