Методику решение задач выпуклого программирования с линейными ограничениями методом приведенного градиента впервые предложил Вульф в 1963 году. Данный метод получил название метод Франка–Вульфа или метод приведенного градиента. В дальнейшем данный метод распространили на решение задач нелинейного программирования с заданными нелинейными ограничениями.
Метод приведенного градиента (в англ. литературе «reduced gradient method») ˗ это итерационный численный метод решения оптимизационных задач, который позволяет определить «условный» экстремум целевой функции (минимальное или максимальное значение)
при наличии заданных ограничений на ее переменные в виде равенств (т.е. определена область допустимых значений)
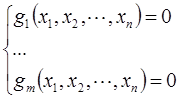
˗ это значения аргумента функции (управляемые параметры) на вещественной области при котором значение целевой функции стремится к «условному» экстремуму. Применение названия «условный» экстремум связано с тем, что на переменные наложено дополнительное условие, которое ограничивает область допустимых значений при поиске экстремума функции.
Метод приведенного градиента основан на сокращении размерности задачи с помощью представления всех переменных через множество зависимых (Y) и независимых (X) переменных. Количество зависимых (Y) переменных должно соответствовать размерности системы ограничений (1…m). В результате задача поиска экстремума функции переписывается следующим образом:
Целевая функция:
Система уравнений с ограничениями:
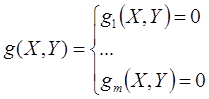
В соответствии с рассматриваемым методом вектор столбец независимых (X) переменных определяется на каждом шаге итерационного расчета используя следующее выражение:
В зависимости от условия поиска (поиск максимального или минимального значения целевой функции) используется либо знак «+», либо знак «-».
Направление движение определяется градиентом функции через производные целевой функции по независимым (X) переменным. Следует отметить, что зависимые (Y) переменные целевой функции является неявной функцией от независимых (X) переменных в системе уравнений, которые определяют ограничения задачи. Запишем производную целевой функции по независимым (X) переменным с учетом неявной зависимости:
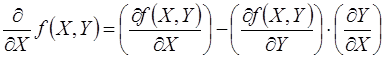
где производные в скобках определяются с учетом явной зависимости целевой функции от зависимых (Y) и независимых (X) переменных.
Производную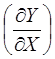 
определяем аналогично, используя систему уравнений с ограничениями 
где производные в скобках определяются с учетом явной зависимости системы уравнений с ограничениями от зависимых (Y) и независимых (X) переменных.
В результате получили выражение для определения приведенного градиента функции:
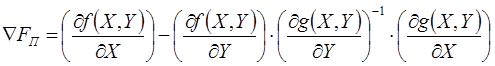
В рассматриваемой задачи используется понятие приведённого градиента целевой функции 
, который определяется проекцией градиента целевой функции 
на плоскость проведенной к нелинейной поверхности, описываемой уравнениями с ограничениями задачи 
. Следует отметить, что градиент и антиградиент 
ортогонален поверхности проведенной к целевой функции f(x) в точке x. Идея градиентных методов основана на том, что антиградиент функции 
указывает направление наиболее быстрого ее убывания в окрестности точки 
, в которой он вычислен. Поэтому, если из некоторой текущей точки перемещаться в направлении антиградиента функции 
, то функция f(x) будет убывать.
Рис.1. График линий равного уровня функции f(x) с пояснением метода приведенного градиента
Величина шага выбирается из условия поиска экстремума целевой функции f(х) в направлении движения, т. е. в результате решения задачи одномерной оптимизации:
В последнем выражении знак «+» используется если по условиям задачи необходимо найти максимум целевой функции, а знак «-» используется если по условиям задачи необходимо найти минимум целевой функции.
В дальнейшем на каждом шаге расчета определяются независимые (X) переменные, которые используются для определения зависимых (Y) переменных используя систему уравнений с ограничениями.
Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета (несколько критериев):
- траектория поиска остается в малой окрестности текущей точки поиска:
- приращение целевой функции не меняется:
- градиент целевой функции в точке локального минимума обращается в нуль:
Методика расчета
1 шаг: Разделяем вектор столбец неизвестных на вектор-столбец зависимых (Y) и независимых (X) переменных. В результате задача поиска экстремума функции переписывается следующим образом:
Целевая функция:
Система уравнений с ограничениями:
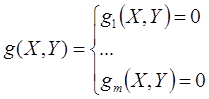
2 шаг: Определение аналитических соотношений (в символьном виде) для вычисления приведенного градиента функции:
› Определение производной целевой функции по независимым переменным с учетом явной зависимости функции от независимых (X) и зависимых (Y) переменных
; 
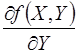
› Определение производной системы уравнений, записанной для ограничений, по независимым переменным с учетом явной зависимости функции от независимых (X) и зависимых (Y) переменных
; 
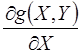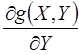
3 шаг: Задаем начальное приближение для вектор-столбца независимых (X) переменных
Далее выполняется итерационный процесс.
4 шаг: Определяем вектор-столбец зависимых (Y) переменных на текущем шаге расчета используя систему уравнений с ограничениями.
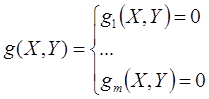
5 шаг: Определяем значение приведенный градиент для текущего шага расчета.
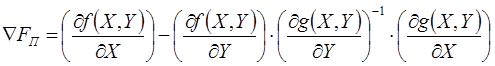
6 шаг: определяем шаг расчета из условия поиска экстремума для следующей функции 
(решения задачи одномерной оптимизации).
7 шаг: определяем вектор-столбец независимых (X) переменных на следующем шаге расчета:
8 шаг: проверяем критерии останова итерационного процесса:
- траектория поиска остается в малой окрестности текущей точки поиска;
- приращение целевой функции не меняется;
- градиент целевой функции в точке локального минимума обращается в нуль.
В противном случае возвращаемся к «шагу 4» и продолжаем итерационный расчет.
Таким образом, в соответствии с представленным методом происходит движение из любой допустимой точки вдоль линии (области) ограничения до тех пор, пока не достигается экстремум целевой функции f(x) (максимум или минимум функции).
