Метод множителей Лагранжа (в англ. литературе «LaGrange's method of undetermined multipliers») ˗ это численный метод решения оптимизационных задач, который позволяет определить «условный» экстремум целевой функции (минимальное или максимальное значение)
при наличии заданных ограничений на ее переменные в виде равенств (т.е. определена область допустимых значений)
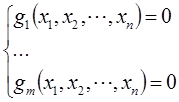
˗ это значения аргумента функции (управляемые параметры) на вещественной области при котором значение функции стремится к экстремуму. Применение названия «условный» экстремум связано с тем, что на переменные наложено дополнительное условие, которое ограничивает область допустимых значений при поиске экстремума функции.
Метод множителей Лагранжа позволяет задачу поиска условного экстремума целевой функции на множестве допустимых значений преобразовать к задаче безусловной оптимизации функции.
В случае если функции 
и 
непрерывны вместе со своими частными производными, то существуют такие переменные λ не равные одновременно нулю, при которых выполняется следующее условие:
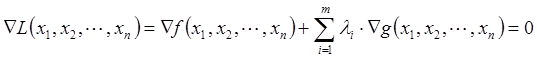
Таким образом, в соответствии с методом множителей Лагранжа для поиска экстремума целевой функции на множестве допустимых значений составляю функцию Лагранжа L(х, λ), которую в дальнейшем оптимизируют:
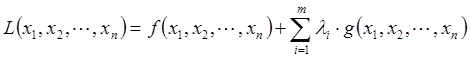
где λ ˗ вектор дополнительных переменных, называемых неопределенными множителями Лагранжа.
Таким образом, задача нахождения условного экстремума функции f(x) свелась к задаче поиска безусловного экстремума функции L(x, λ).
Далее в соответствии с методом определяют частные производные функции Лагранжа:
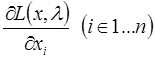и 
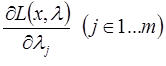
Необходимое условие экстремума функции Лагранжа задается системой уравнений (система состоит из «n + m» уравнений):
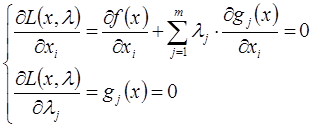
Решение данной системы уравнений позволяет определить аргументы функции (Х), при которых значение функции L(x, λ), а также значение целевой функции f(x) соответствуют экстремуму.
Величина множителей Лагранжа (λ) имеет практический интерес в случае, если ограничения представлены в форме со свободным членом уравнения (константой). В этом случае можно рассматривать дальнейшее (увеличение/уменьшение) значения целевой функции за счет изменения значения константы в системе уравнения 
. Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы.
Существует несколько способов определения характера экстремума полученной функции:
Первый способ: Пусть 
– координаты точки экстремума, а 
- соответствующее значение целевой функции. Берется точка 
, близкая к точке , и вычисляется значение целевой функции 
:
- Если 
, то в точке 
имеет место максимум.
- Если 
, то в точке имеет место минимум.
Второй способ: Достаточным условием, из которого можно выяснить характер экстремума, является знак второго дифференциала функции Лагранжа. Второй дифференциал функции Лагранжа определяется следующим образом:
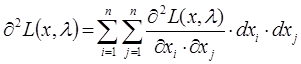
Если в заданной точке 
, то целевая функция f(x) имеет в данной точке условный минимум, если же 
, то целевая функция f(x) имеет в данной точке условный максимум.
Третий способ: Также характер экстремума функции можно выяснить рассмотрев гессиан функции Лагранжа. Матрица Гессе представляет собой симметричную квадратную матрицу вторых частных производных функции в точке 
, в которой элементы матрицы симметричны относительно главной диагонали.
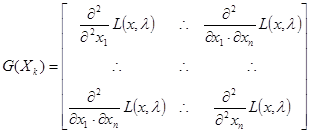
Для определения типа экстремума (максимум или минимум функции) можно воспользоваться правилом Сильвестра:
1. Для того, чтобы второй дифференциал функции Лагранжа был знакоположителен 
необходимо, чтобы угловые миноры функции были положительными 
. При таких условиях функция в этой точке имеет минимум.
2. Для того, чтобы второй дифференциал функции Лагранжа был знакоотрицателен 
, необходимо, чтобы угловые миноры функции чередовались, причем первый элемент матрицы должен быть отрицательнsv 
. При таких условиях функция в этой точке имеет максимум.
Под угловым минором понимаем минор, расположенный в первых k строках и k столбцах исходной матрицы.
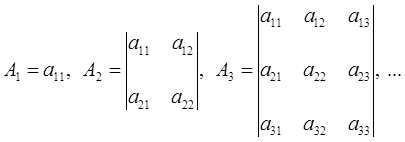
Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных методов решения задачи. Однако задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной задачи поиска экстремума. Такие методы называются непрямыми. Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций.
Методика расчета
1 шаг: Определяем функцию Лагранжа из заданной целевой функции и системы ограничений:
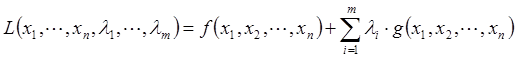
2 шаг: Определение аналитических соотношений (в символьном виде) для поиска безусловного экстремума функции L(x, λ).
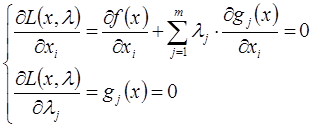
3 шаг: Решаем полученную систему линейных или нелинейных уравнений, используя соответствующие методы решения.
4 шаг: Определяем характер экстремума (максимум или минимум целевой функции) по любому из представленных выше методов.
