Задача разложения правильной дроби на простейшие состоит в следующем: некоторую правильную рациональную дробь необходимо представить в виде суммы простейших рациональных дробей.
Простыми дробями называются рациональные дроби вида 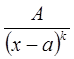 или
или 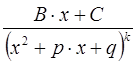 , где
, где ![]() , а квадратный трехчлен
, а квадратный трехчлен ![]() не имеет действительных корней, т.е. дискриминант квадратного уравнения меньше нуля
не имеет действительных корней, т.е. дискриминант квадратного уравнения меньше нуля ![]() .
.
Правильной рациональной дробью называется дробь вида 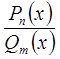 , где числитель и знаменатель представлен в виде многочлена, а степень числителя ниже степени знаменателя
, где числитель и знаменатель представлен в виде многочлена, а степень числителя ниже степени знаменателя ![]() .
.
В случае если степень числителя выше степени знаменателя ![]() , то дробь называют неправильной. Если дробь является неправильной, то необходимо разделить числитель на знаменатель (по правилу деления многочленов), и представить дробь в виде суммы многочлена
, то дробь называют неправильной. Если дробь является неправильной, то необходимо разделить числитель на знаменатель (по правилу деления многочленов), и представить дробь в виде суммы многочлена ![]() и правильной рациональной дроби
и правильной рациональной дроби ![]() :
:

Любая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых рациональных дробей следующим образом:
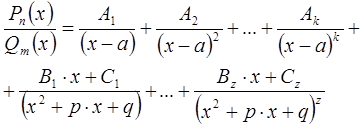
Коэффициенты такого преобразованного выражения определяются методом неопределенных коэффициентов. Метод неопределённых коэффициентов ― это метод, используемый в математике для разложения искомой функции в виде линейной комбинации конечного или бесконечного набора базовых функций.
Рассмотрим прием разложения правильной рациональной дроби в виде суммы простейших дробей с неопределенными коэффициентами.
Алгоритм метода неопределенных коэффициентов
Чтобы разложить правильную рациональную дробь 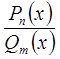 на простые дроби, необходимо выполнить следующие действия.
на простые дроби, необходимо выполнить следующие действия.
1. Разложить знаменатель ![]() на линейные и квадратные множители, которые не имеют действительных корней.
на линейные и квадратные множители, которые не имеют действительных корней.
2. Записать разложение дроби 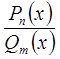 в аналитической форме в виде простейших дробей с неопределенными коэффициентами.
в аналитической форме в виде простейших дробей с неопределенными коэффициентами.
В случае если в знаменателе присутствует сомножитель вида ![]() , то дробь раскладывается в следующем виде:
, то дробь раскладывается в следующем виде:
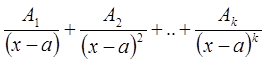
В случае если в знаменателе присутствует сомножитель вида ![]() , то дробь раскладывается в следующем виде:
, то дробь раскладывается в следующем виде:
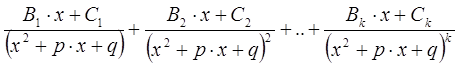
3. Преобразуем полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.
4. Составляем систему уравнений из условия равенства коэффициентов при соответствующих степенях знаменателя в связи с тем, что аналитическая дробь с неизвестными коэффициентами равна исходной дроби. В результате получим систему линейных алгебраических уравнений относительно неизвестных коэффициентов разложения данной рациональной функции на сумму простейших. Решаем полученную систему уравнений для определения значений неопределённых коэффициентов. Следует отметить, что система уравнений для определения неизвестных коэффициентов разложения всегда имеет единственное решение.
Таким образом, выполняется разложение правильной рациональной дроби на сумму простых дробей. Рассмотрим задачи, которые решаются методом неопределённых коэффициентов.
Задача. Разложение дроби на простейшие
Необходимо представить правильную дробь в виде суммы простейших дробей. Для простоты задачи знаменатель рассматриваемой дроби представлен в виде произведения множителей.

1. Запишем разложение дроби в аналитической форме в виде простейших дробей с неопределенными коэффициентами.
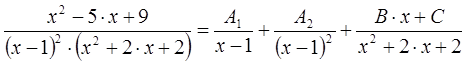
где переменные A,B,C - неопределённые коэффициенты
2. Преобразуем полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю.
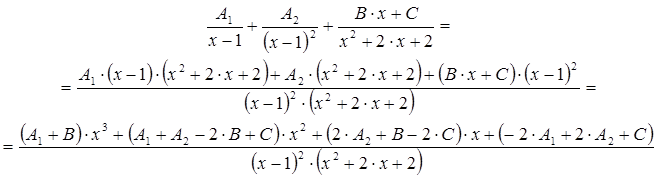
3. Составляем систему уравнений из условия равенства коэффициентов при соответствующих степенях знаменателя.
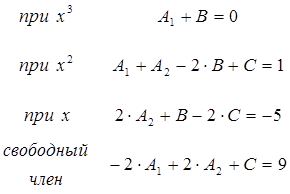
Решая данную систему, получим, что неопределённые коэффициенты определяются следующим образом:
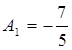 ;
; ![]() ;
; 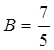 ;
; 
Таким образом, исходная рациональная дробь раскладывается на сумму простых дробей следующим образом:
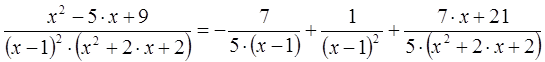
Данный метод может использоваться как при аналитических выкладках, так и при компьютерном программировании для автоматизации процесса.