Метод градиентного спуска (метод градиента) (в англ. литературе «gradient-search method») – это итерационный численный метод (первого порядка) решения оптимизационных задач, который позволяет определить экстремум (минимум или максимум) целевой функции:
- это значения аргумента функции (управляемые параметры) на вещественной области.
В соответствии с рассматриваемым методом экстремум (максимум или минимум) целевой функции определяют в направлении наиболее быстрого возрастания (убывания) функции, т.е. в направлении градиента (антиградиента) функции. Градиентом функции в точке называется вектор, проекциями которого на координатные оси являются частные производные функции по координатам:
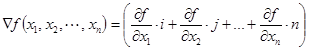
где i, j, n - единичные векторы, параллельные координатным осям.
Частные производные характеризуют изменение функции по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в заданной окрестности точки.
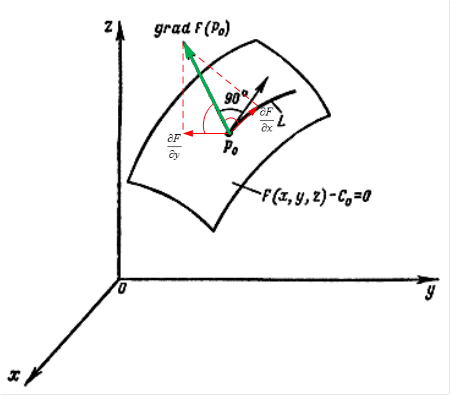
Рис.1. Градиент к поверхности функции
Градиент в базовой точке 
строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиент), соответственно, показывает направление наискорейшего убывания функции.
Модуль градиента определяется в соответствии со следующей формулы:
Углы наклона этого вектора к направлению координатных осей х, у, z определяются исходя из соотношений в прямоугольном треугольнике (косинус угла):
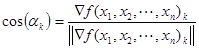
В общем случае процесс нахождения экстремума (минимума или максимума) функции является итерационной процедурой, которая записывается в векторной форме следующим образом:
«+» используется, когда ищется максимум функции;
«-» используется, когда ищется минимум функции.
Градиент (антиградиент) дает только направление спуска, но не величину шага. В общем случае один шаг не дает точку экстремума, поэтому процедура спуска должна применяться несколько раз. В точке минимума все компоненты градиента равны нулю. Ниже на рисунке представлена графическая интерпретация метода градиентного спуска.
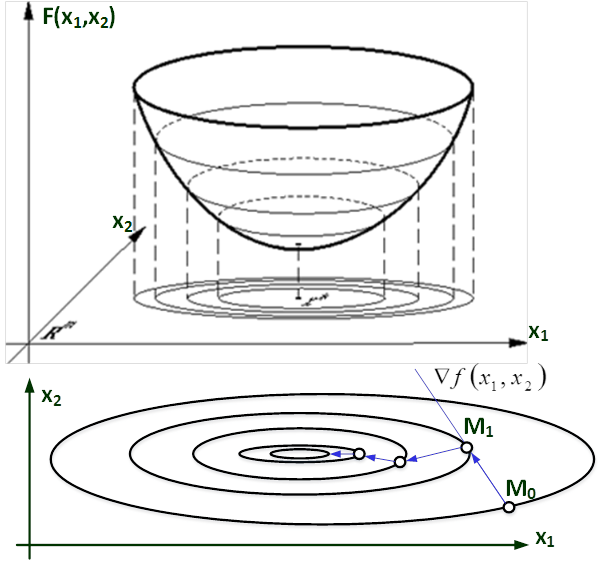
Рис.2. Геометрическая интерпретация градиентного метода
Величина рабочего шага в направлении градиента зависит от величины градиента и от коэффициента пропорциональности шага. Величина шага расчета сильно влияет на эффективность метода расчета. В данном методе шаг расчета выбирается двумя способами:
- постоянный шаг расчета;
- дробным шагом, то есть длина шага в процессе спуска делится на некоторое число. Например, в случае поиска минимума функции можно воспользоваться следующей идеологией: в случае 
, то 
, в противном случае шаг расчета остается без изменения 
Нормированная запись уравнения
Большей эффективностью обладает другой вариант записи уравнения, когда шаг по переменной определяется направляющими косинусами градиента. Данный метод базируется на том, что производная целевой функции пропорциональна косинусу угла, образуемого вектором градиента с i-й осью координат. В связи с этим алгоритм градиентного поиска преобразуют к следующему виду:
где 
- единичный вектор направления, который определяется по формуле:
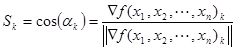
- модуль градиента определяет скорость возрастания или убывания функции в направлении градиента или антиградиента:
– константа, определяющая размеры шага и одинаковая для всех i-х направлений.
Величина шага, выбираемая в направлении градиента (антиградиента) целевой функции, зависит от вида поверхности. В случае если шаг слишком мал, то потребуются продолжительные расчеты; в случае если шаг слишком велик, то можно проскочить оптимум. В данном методе используется дробный шаг расчета, который выбирается следующим образом:
- если угол наклона градиента меньше 30 градусов, то шаг расчета увеличить на некоторое число 
;
- если угол наклона градиента находится в диапазоне от 30 до 60 градусов, то шаг расчета не изменяется ;
- если угол наклона градиента больше 60 градусов, то шаг расчета делится на некоторое число 
.
Итерационный процесс расчета продолжается до тех пор, пока не будут выполнены некоторые критерии останова:
- траектория поиска остается в малой окрестности текущей точки поиска:
- приращение целевой функции не меняется:
- градиент целевой функции в точке локального минимума обращается в нуль:
Метод градиента вместе с его многочисленными модификациями является распространенным и эффективным методом поиска оптимума исследуемых объектов. Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции. Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек.
Методика расчета.
- 1 шаг: Определение аналитические выражения (в символьном виде) для вычисления градиента функцииÑf(V), длины вектора градиента |Ñf(V)| и единичного вектора t(V)
градиент рассматриваемой функции:
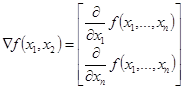
единичный вектор направления:
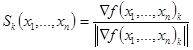
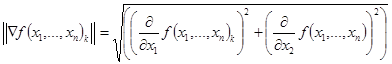
- 2 шаг: Задаем начальное приближение
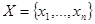
Далее выполняется итерационный процесс.
- 3 шаг: Вычисление координат единичного вектора
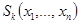по формуле, полученной на шаге 1, и определение координат новой точки при движении по направлению единичного вектора как функция от шага расчета.
4 шаг: Определяем шаг расчета: постоянный или дробный шаг расчета.
5 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета методом градиентного спуска:
6 шаг: проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
