Метод сопряженных градиентов (в англ. литературе «conjugate gradient method») - это итерационный численный метод (первого порядка) решения оптимизационных задач, который позволяет определить экстремум (минимум или максимум) целевой функции:
- это значения аргумента функции (управляемые параметры) на вещественной области.
В соответствии с рассматриваемым методом экстремум (максимум или минимум) целевой функции определяют в направлении наиболее быстрого возрастания (убывания) функции, т.е. в направлении градиента (антиградиента) функции. Градиентом функции в точке называется вектор, проекциями которого на координатные оси являются частные производные функции по координатам:
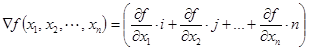
где i, j,…, n - единичные векторы, параллельные координатным осям.
Градиент в базовой точке 
строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиент), соответственно, показывает направление наискорейшего убывания функции.
Метод сопряженных градиентов является дальнейшим развитием метода наискорейшего спуска, который сочетает в себе два понятия: градиент целевой функции и сопряженное направление векторов. В общем случае процесс нахождения минимума функции является итерационной процедурой, которая записывается в векторной форме следующим образом:
где знак «+» используется для поиска максимума функции, а знак «-» используется для поиска минимума функции.
- единичный вектор сопряженных направлений, который определяется по формуле:
Существует несколько способов определения значений весовых коэффициентов (переменная 
), которые используются для определения сопряженного направления.
В качестве первого способа рассматривают определение весового коэффициента по формуле Флетчера-Ривса (Fletcher–Reeves):
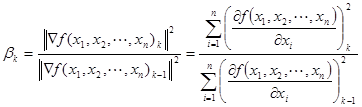
- модуль градиента определяет скорость возрастания или убывания функции в направлении градиента или антиградиента соответственно.
В качестве второго способа рассматривают определение весового коэффициента по формуле Полака–Райбера (Polak-Ribiere):
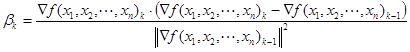
В соответствии с представленными выражениями новое сопряженное направление получается сложением градиента (антиградиента) в точке поворота и предыдущего направления движения, умноженного на коэффициент. Таким образом, метод сопряженных градиентов формирует направление поиска к оптимальному значению используя информацию о поиске полученную на предыдущих этапах спуска. Следует отметить, что сопряженные направления P[0], P[1], ..., P[k-1] вычисляют с помощью формулы Флетчера-Ривса, которая позволяет построить сопряженные векторы относительно некоторой симметрической матрицы для произвольно заданной функции.
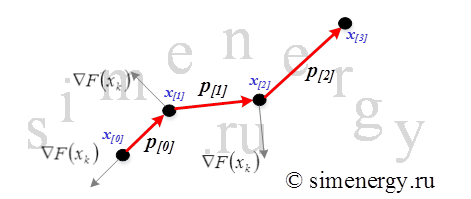
Рис.1. Траектория спуска в методе сопряженных градиентов (поиск минимума)
Геометрический смысл метода сопряженных градиентов состоит в следующем: из заданной начальной точки х[0] осуществляется спуск в направлении р[0] (градиента или антиградиента) в новую точку х[1], в которой определяется вектор-градиент функции. Поскольку х[1] является точкой минимума функции в направлении р[0], то вектор-градиент функции в точке х[1] ортогонален вектору р[0]. Затем определяется вектор р[1] который ортогонален относительно некоторой симметрической матрицы вектору р[0]. В результате осуществляется спуск вдоль найденного направления в новую точку х[2].
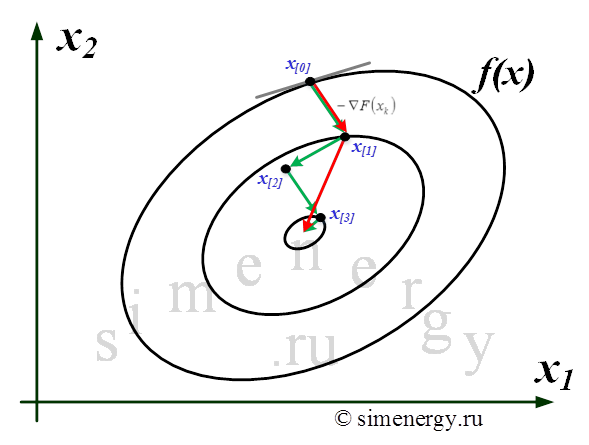
Рис.2. Траектория движения к точке экстремума при использовании метода наискорейшего спуска (зелёная ломаная) и метода сопряжённых градиентов (красная ломаная).
Следует отметить, что через каждые n + 1 шагов необходимо выполнять рестарт алгоритмической процедуры (n – размерность пространства поиска). Рестарт алгоритмической процедуры необходим, чтобы забыть последнее направление поиска и стартовать алгоритм заново в направлении скорейшего спуска.
Величина шага выбирается из условия минимума целевой функции f(х) в направлении движения, т. е. в результате решения задачи одномерной оптимизации в направлении градиента или антиградиента:
Другими словами, величину шага 
определяют при решении данного уравнения:
Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета (несколько критериев):
- траектория поиска остается в малой окрестности текущей точки поиска:
- приращение целевой функции не меняется:
- градиент целевой функции в точке локального минимума обращается в нуль:
Метод сопряженных градиентов является методом первого порядка, но при этом обладает квадратичной скоростью сходимости, как Ньютоновские методы расчета. Метод градиента вместе с его многочисленными модификациями является распространенным и эффективным методом поиска оптимума исследуемых объектов. Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции. Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек.
Методика расчета
- 1 шаг:Определение аналитические выражения (в символьном виде) для вычисления градиента функции
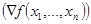
- 2 шаг: Задаем начальное приближение
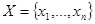
Далее выполняется итерационный процесс.
- 3 шаг:Определяется необходимость рестарта алгоритмической процедуры для обнуления последнего направления поиска. В результате рестарта поиск осуществляется заново в направлении скорейшего спуска.
- 4 шаг: Вычисление координат единичного вектора
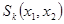по формуле, полученной на шаге 1, и определение координат новой точки при движении по направлению единичного вектора как функция от шага расчета.
Вычисление весового коэффициента и единичного вектора сопряженных направлений на текущем шаге расчета (формула Флетчера-Ривса):
- для первого шага расчета 
весовой коэффициент не вычисляется (или в случае рестарта алгоритма), а единичный вектор сопряженных направлений определяется следующим образом:
- для последующих шагов расчета 
весовой коэффициент и единичный вектор сопряженных направлений вычисляются по следующим соотношениям:
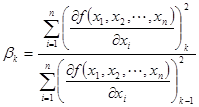
- 5 шаг: определяем шаг расчета из условия поиска экстремума для следующей функции
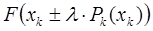(решения задачи одномерной оптимизации).
- 6 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета:
где знак «+» используется для поиска максимума функции, а знак «-» используется для поиска минимума функции;
- 7 шаг:проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
