Аппроксимация экспериментальной зависимости. Линейная регрессия. Статистические критерии оценки линейной регрессии.

Аппроксимация метод приближения, при котором некоторые величины (или объекты) выражаются через другие, более простые величины (или объекты). Таким образом, аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к более простым математическим моделям, которые более удобны к изучению.

В качестве исходных данных задан массив экспериментально полученных значений двух измеряемых величин: y1, y2, y3, … yn и x1, x2, x3, … xn , которые связаны некоторой функциональной зависимостью y=f(x), вид которой заранее не известен. Каждая пара совместно измеренных значений (xi, yi) определяет положение некоторой точки. Величины xi и yi не свободны от погрешностей, поэтому определяемые ими точки не лежат точно на какой-то кривой, а образуют некоторое облако с нечеткими границами. Необходимо определить регрессионную кривую y=f(x), проходящую через данную область точек.

Линейная регрессия (англ. Linear regression) — модель зависимости одной переменной y от другой или нескольких других переменных x (факторов, регрессоров, независимых переменных)  с линейной функцией зависимости:

где переменные «a» и «b» – параметры зависимости y=f(x).

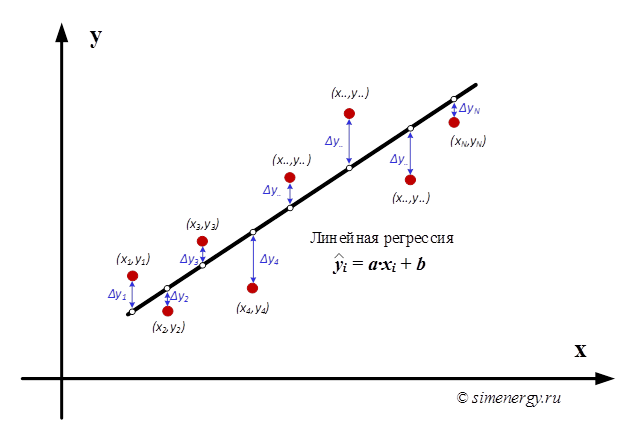
Рис.1. Линейная регрессия

Выбор параметров «a» и «b» должен быть выполнен таким образом, чтобы искомая теоретическая кривая y=f(x) наилучшим образом проходила через заданную область точек. Существуют различные критерии выбора наилучшего соответствия экспериментальных точек и регрессионной кривой. Одним из наиболее общих способов отыскания оценок истинных значений искомых параметров является разработанный Лежандром и Гауссом метод наименьших квадратов (МНК).

Примечание: Метод получения оценок параметров оптимальной прямой с помощью минимизации суммы квадратов отклонений называется Методом Наименьших Квадратов (сокращенно МНК) или Ordinary Least Squares (сокращенно OLS), а полученные оценки параметров называются МНК- или OLS-оценками.

Суть метода наименьших квадратов заключается в том, чтобы подобрать такие значения коэффициентов, при которых сумма квадратов отклонений измеренных в эксперименте значений (xi, yi) от искомой кривой y=f(x) была бы минимальна.

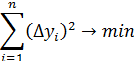
Обозначим функцию, которую требуется минимизировать через переменную RSS (Resudiual Sum of Squares) – остаточная сумма квадратов отклонений.

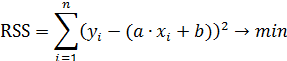
Сумма квадратов отклонений является функцией двух независимых переменных: «a» и «b». Для нахождения минимума суммы квадратов отклонений функции необходимо приравнять к нулю ее частные производные по «a» и «b».

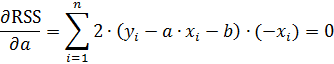
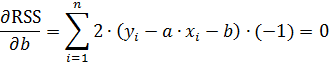
Преобразуем полученную систему выражений

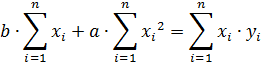
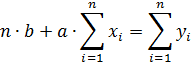
Перепишем систему уравнений в следующем виде

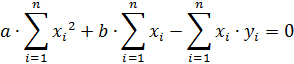
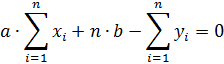
Из последнего выражения определяем параметр «b»

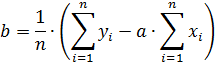
Далее подставляем полученное выражение в первое уравнение. Решая полученную систему уравнение, определим неизвестные параметры «a» и «b» (коэффициенты регрессионной кривой)

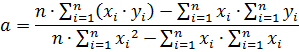
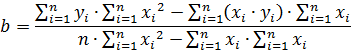
С учетом найденных коэффициентов «a» и «b» строится регрессионная кривая по следующему выражению:

где переменная  - значения регрессионной кривой.

После того, как найдено уравнение линейной регрессии, проводится оценка, как уравнения в целом, так и отдельных его параметров.

П.1.  Средняя ошибка аппроксимации

Общей характеристикой качества построенной регрессии (не только парной и линейной, но и любой другой) является средняя ошибка аппроксимации, которая показывает среднее отклонение расчетных значений от фактических. Средняя ошибка аппроксимации рассчитывается по формуле:

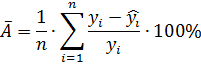
где переменная   - значения регрессионной кривой , переменная   – значения из массива исходных данных, а переменная 𝑛  - количество измерений.

Значение средней ошибки аппроксимации до 15% свидетельствует о хорошо подобранной модели уравнения.

П.2. Стандартная ошибка регрессии

Стандартная ошибка регрессии (Standard Error) - это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. 

Стандартная ошибка регрессии определяется как корень квадратный из остаточной дисперсии

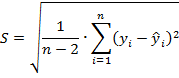
где переменная   - значения регрессионной кривой , переменная   – значения из массива исходных данных, а переменная 𝑛 - количество измерений.

В знаменателе формулы используется выражение , которое соответствует количеству степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1).

Значение стандартной ошибки позволяет увидеть степень отклонения значений, полученных с помощью регрессии, от фактически наблюдаемых, и таким образом оценить точность соответствующей модели.

Значение стандартной ошибки измеряет степень отличия реальных значений Y от уравнения линейной регрессии. Малая стандартная ошибка оценки, полученная при регрессионном анализе, свидетельствует, что все точки данных находятся очень близко к прямой регрессии. Если стандартная ошибка оценки велика, точки данных могут значительно удаляться от прямой.

П.3. Интервальные оценки параметров уравнения регрессии

Помимо определения качества уравнения регрессии в целом, также проводится оценка отдельных его параметров, а именно интервальные оценки параметров уравнения регрессии (Standard Error Coefficients). 

Уравнение регрессии (y=ax+b) содержит коэффициенты «a» и «b», которые определяются теоретически по исходным данным. В результате полученное уравнение с определённой точностью описывает изменение экспериментальных данных. Поскольку уравнение регрессии может быть использовано при анализе и прогнозировании необходимо для данных коэффициентов уметь определять доверительные интервалы, в границах которых с определенной вероятностью находятся действительные значения параметров. 

П.1. Доверительный интервал для коэффициента регрессии «a» определяется следующим соотношением

где переменная   -  стандартная ошибка оценки коэффициента регрессии «a»

Стандартная ошибка определяется по следующему выражению:

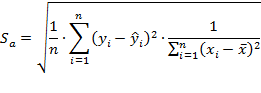
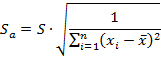
где переменная   определяется из таблицы критических точек распределения Стьюдента в зависимости от уровня ошибки , а  - среднее значение параметра.

П.2. Доверительный интервал для коэффициента регрессии «b» определяется следующим соотношением

где переменная   – стандартная ошибка оценки свободного члена уравнения регрессии (коэффициента регрессии «b»)

Стандартная ошибка определяется по следующему выражению:

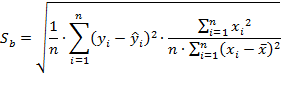
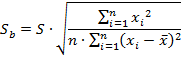
где переменная   определяется из таблицы критических точек распределения Стьюдента в зависимости от уровня ошибки  , а  - среднее значение параметра.

Переменная  определяется из таблицы критических точек распределения Стьюдента. Для этого в качестве исходных данных выбирается уровень ошибки (0,10 или 0,05 или 0,01 или другие значения в расширенной таблице), а далее выбирается значение переменной  в зависимости от количества степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1).

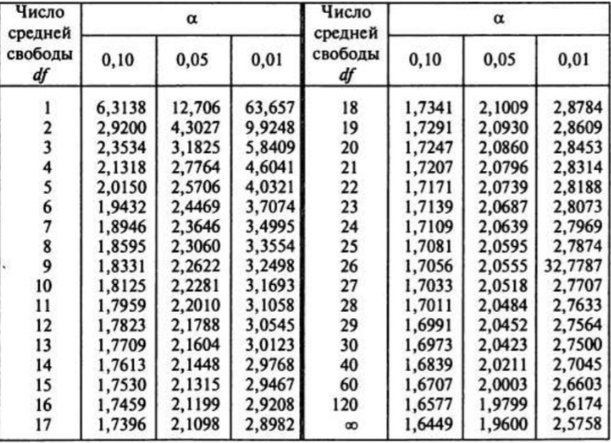
Рис.2. Таблица критических точек распределения Стьюдента в зависимости от уровня ошибки

Другой способ проверки статистической значимости параметров регрессии непосредственно не связан с построением доверительных интервалов. Проверка гипотезы осуществляется с помощью критерия Стьюдента (t-критерий Стьюдента). На основе полученных значений параметров регрессионной кривой, а также рассчитанных стандартных ошибок оценки коэффициента регрессии определяются эмпирические значения t-статистик:

где переменные «a» и «b» -  значение параметра, а переменные  и  - стандартная ошибка оценки коэффициента регрессии.

Далее полученные значения сравниваются со значениями , которые берутся из таблицы критических точек распределения Стьюдента при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1). Если расчетное значение превышает по абсолютной величине табличное значение, то соответствующий коэффициент является статистически значимым с заданной доверительной вероятностью.

П.4. Линейный коэффициент корреляции Пирсона

Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя случайными величинами. Для случайных величин X и Y выборочный коэффициент корреляции определяется по формуле:

Параметры  и  - стандартные отклонения, соответствующие случайным величинам X и Y, а cov(X,Y) – коэффициент ковариации переменных X и Y.

где 𝑥𝑖, 𝑦𝑖 – элементы выборки, n – размер выборки, а  - среднее значение параметров.

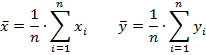
Используя формулы средних перепишем выражение для определения линейного коэффициента корреляции Пирсона. 

Все значения коэффициента корреляции находятся в интервале от -1 до +1. Близость к нулю абсолютного значения  обычно означает слабую линейную взаимосвязь между переменными. В случае если абсолютное значение   близко к единице, то это говорит о сильной линейной взаимосвязи между ними. Коэффициент корреляции отражает тесноту именно линейной связи между переменными, т.е. близость его к нулю свидетельствует об отсутствии именно линейной зависимости. Однако при этом переменные могут иметь связь другого вида: нелинейную.

Также формула для определения коэффициента корреляции Пирсона может быть использована для анализа двух других случайных величин: значений из массива исходных данных и значений регрессионной кривой  .

П.5. Коэффициент детерминации

Следующим критерием оценки качества точности уравнения регрессии является коэффициент детерминации (Coefficient of determination). Коэффициент детерминации определяется как отношение объясненной ошибки (SSR) к общей ошибки (SST).

Коэффициент детерминации представляет собой квадрат корреляционного отношения.

Коэффициент детерминации является удобной оценкой степени связи между регрессивной линией и фактическими данными. Коэффициент детерминации показывает, какая доля общей вариации исследуемого показателя определяется (детерминируется) совокупным влиянием функции регрессии (т. е. выбранными нами объясняющими показателями).

Данное выражение переписывают в другом виде в случае линейной регрессии, т.к. в случае линейной регрессии с константой справедливо следующее соотношение:

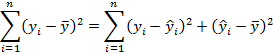
В результате для линейной регрессии с константой коэффициент детерминации определяется следующим образом:

где 𝑦𝑖 – элементы выборки, n – размер выборки,  - среднее значение параметров, а  – значения функции линейной регрессии .

Примечание: Еще раз обращаем Ваше внимание, что данная запись справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.

Коэффициент детерминации измеряет долю изменчивости Y, которую можно объяснить с помощью информации об изменчивости (разнице значений) независимой переменной X. Коэффициент детерминации изменяется в диапазоне от −∞ до 1.

Если коэффициент детерминации равен 1, это соответствует идеальной модели, когда все точки наблюдений лежат точно на линии регрессии, т.е. сумма квадратов их отклонений равна 0.

Если коэффициент детерминации равен 0, это означает, что связь между переменными регрессионной модели отсутствует, и вместо нее для оценки значения выходной переменной можно использовать простое среднее ее наблюдаемых значений.

Так же следует обратить внимание, что в случае линейной регрессии коэффициент корреляции значений из массива исходных данных  и значений регрессионной кривой равен квадратному корню из коэффициента детерминации :

П.6.  Критерий Фишера (F-тест)

Критерий Фишера (F-критерий Фишера) — статистический критерий для оценки значимости различия дисперсий двух случайных выборок, который позволяет оценивать значимость линейных регрессионных моделей. В частности, он используется для проверки целесообразности включения или исключения независимых переменных (признаков) в регрессионную модель.

Критерий Фишера позволяет подтвердить или опровергнуть нулевую гипотезу с помощью сравнения дисперсии двух независимых выборок. Нулевая гипотеза — принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями.

Для определения статистической значимости в начале рассчитывается значение F-критерия Фишера. Фактическое значение статистики Фишера равно отношению удельных (рассчитанных на одну степень свободы) факторной и остаточной дисперсий:

где n – объём выборки, m – число параметров «Х» в уравнении регрессии.

Затем значение F-критерия Фишера сравнивают с критическим (или табличным) значением. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл (a; k1; k2), где k1 = m, где m – это количество факторов в построенной регрессионной модели (число степеней свободы большей дисперсии), а k2 = n – m – 1, где n – число наблюдений (число степеней свободы меньшей дисперсии).

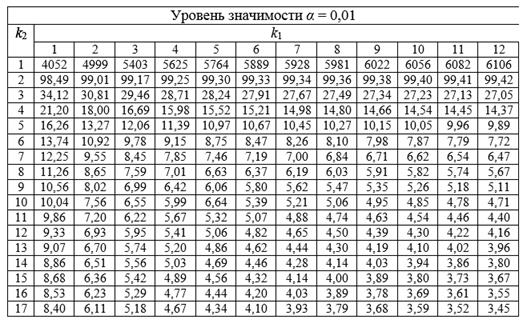
Рис.3. Таблица критических точек распределения Фишера-Снедекора при допустимом уровне значимости a=0.01

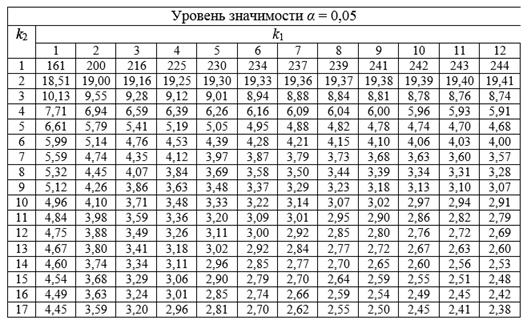
Рис.4. Таблица критических точек распределения Фишера-Снедекора при допустимом уровне значимости a=0.05

В частности, для линейной регрессии (частный F-критерий) переменные k1 = 1, k2 = n – 2 (n – число наблюдений).

Вычисленное значение F – отношения признается достоверным, если оно больше табличного. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, то есть подтверждается статистическая значимость всего уравнения и показателя тесноты связи.

П.1. В случае если значение критерия Фишера больше критического

, то принимается нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.

П.2. В случае если значение критерия Фишера меньше критического

 , то принимается альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска. Соответственно уравнение регрессии считается статистически незначимым и тем самым признается ненадежность уравнения регрессии.

Интерпретация частного F - критерия Фишера следующая: в том случае, когда рассчитанная величина частного F_xi превышает критическое значение, то дополнительное включение фактора x_i в регрессионную модель статистически оправданно и коэффициент регрессии b_i при соответствующем факторе x_i статистически значим. Но если рассчитанная величина F_xi меньше табличного, то дополнительное включение в модель фактора x_i не оправдано, т.к. данный фактор, как и коэффициент регрессии при нём является статистически незначимым.

П.7.Использование нелинейных функций.

Аппроксимация опытных данных также может быть выполнена нелинейными функциями. При этом отдельные нелинейные функции могут быть приведены к линейным функциям путем замены переменных. Соответственно, для этих нелинейных функций, могут использоваться методы для анализа линейной функции. Рассмотрим данные нелинейные функций и методику преобразования данных функций к линейному виду.

П.7.1. Задана исходная нелинейная функция #1 (Степенная функция)

Преобразуем функцию с линейному виду с помощью логарифмирования. В результате получим функцию в следующем виде:

Далее делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент  и коэффициент 

Методика расчета коэффициентов для нелинейной функции #1 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #1.

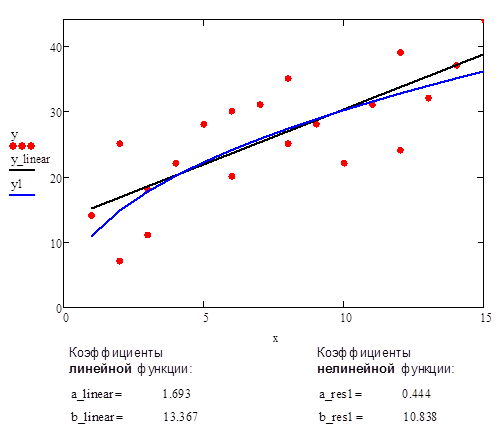
Рис.5. Аппроксимации данных с помощью прямой линии и нелинейной функции #1 (Степенная функция)

 

П.7.2. Исходная нелинейная функция #2 (логарифмическая функция)

Делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент   и коэффициент 

Методика расчета коэффициентов для нелинейной функции #2 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #2.

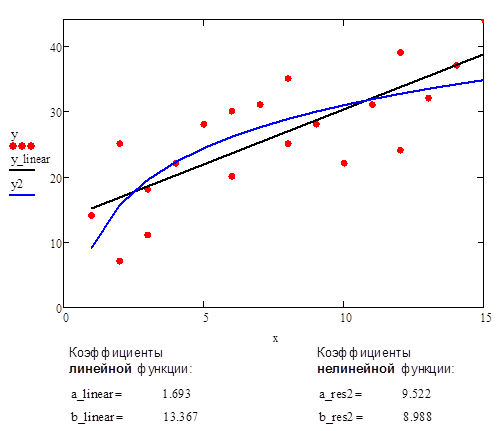
Рис.6. Аппроксимации данных с помощью прямой линии и нелинейной функции #2 (логарифмическая функция)

П.7.3. Исходная нелинейная функция #3 (экспоненциальная функция)

Преобразуемая функция с помощью логарифмирования к следующему виду:

Далее делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент  и коэффициент 

Методика расчета коэффициентов для нелинейной функции #3 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #3.

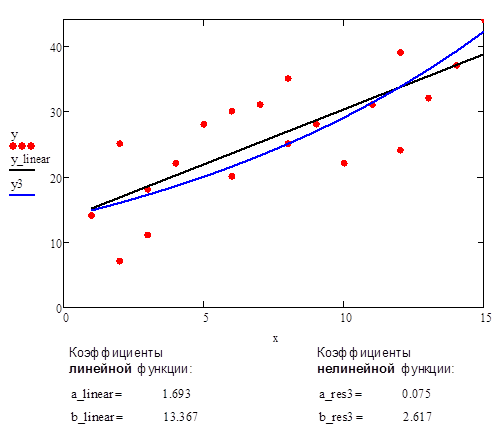
Рис.7. Аппроксимации данных с помощью прямой линии и нелинейной функции #3  (экспоненциальная функция)

П.7.4. Исходная нелинейная функция #4 (экспоненциальная функция)

Преобразуемая функция с помощью логарифмирования к следующему виду:

Далее делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент  и коэффициент 

Методика расчета коэффициентов для нелинейной функции #4 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #4.

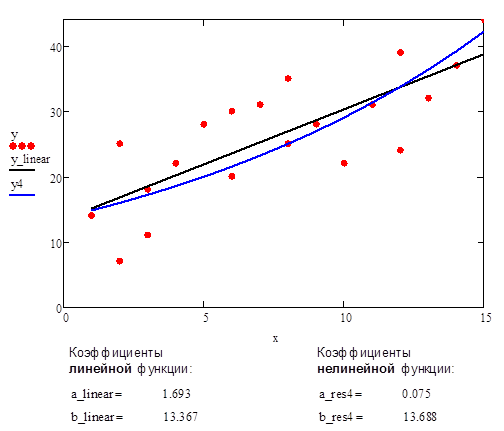
Рис.8. Аппроксимации данных с помощью прямой линии и нелинейной функции #4  (экспоненциальная функция)

П.7.5. Исходная нелинейная функция #5 (гиперболическая функция, гипербола)

Делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент  и коэффициент 

Методика расчета коэффициентов для нелинейной функции #5 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #5.

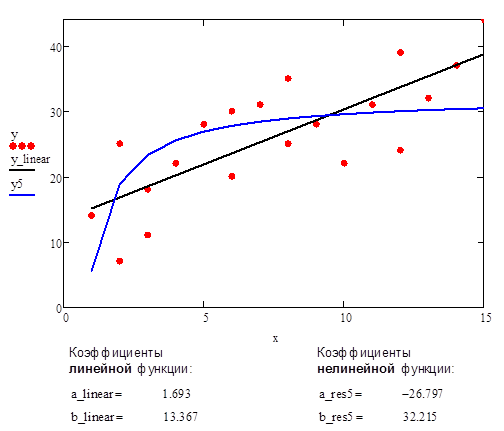
Рис.9. Аппроксимация данных с помощью прямой линии и нелинейной функции #5 (гиперболическая функция, гипербола)

П.7.6. Исходная нелинейная функция #6 (дробно-линейная функция)

Преобразуемая функция к следующему виду:

Далее делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент  и коэффициент 

Методика расчета коэффициентов для нелинейной функции #6 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #6.

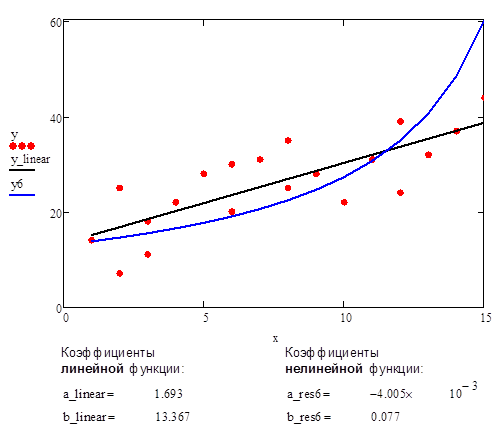
Рис.10. Аппроксимация данных с помощью прямой линии и нелинейной функции #6 (дробно-линейная функция)

 

П.7.7. Исходная нелинейная функция #7 (Дробно-линейная функция)

Преобразуемая функция к следующему виду:

Далее делаем замену переменных и получаем линейную функцию вида:

где переменная , переменная , коэффициент  и коэффициент 

Методика расчета коэффициентов для нелинейной функции #7 следующая:

а) Выполняется расчет коэффициентов  и  для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:  и 

б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов  и :

в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:

В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #7.

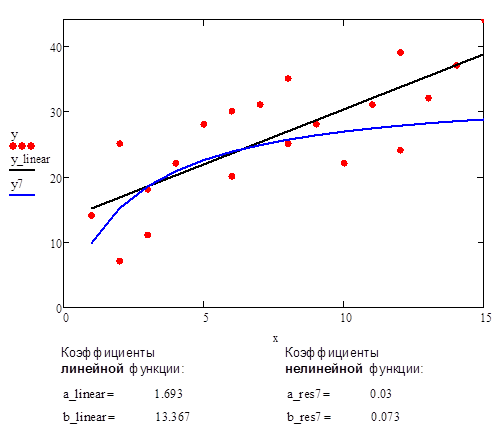
Рис.11. Аппроксимация данных с помощью прямой линии и нелинейной функции #7 (дробно-линейная функция)

Выбор аппроксимирующей функции является важной задачей, так как от выбранной функции в существенной мере зависят количественные характеристики и качественные свойства описания объекта.