Методы экстраполяции

Экстраполяция – это способ предсказания поведения процесса (зависимость изменения данных) в будущем используя известные данные из прошлого. Другими словами, с помощью экстраполяции обобщают заведомо известные данные из прошлого и делают вывод об изменении этих данных в будущем.

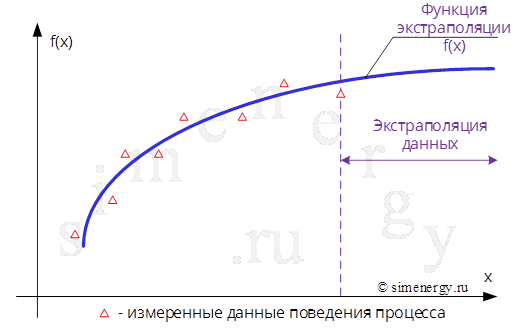
Рис.1. Экстраполяция по данным измерений

Экстраполяция – это операция построения функции за пределами интервалов, на которых эта функция определена.

При использовании метода экстраполяции учитываются следующие допущения:

.- период времени, для которого построена функция, должен быть достаточным для выявлении тенденции развития;

.- анализируемый процесс является устойчиво динамическим и обладает инерционностью, т.е. для значительных изменений характеристик процесса требуется время;

.- не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития.

Методы экстраполяции являются одними из самых распространенных методов прогно­зирования. С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результа­тивности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др. Следует заметить, что метод экстраполяции позволяет предсказать поведение процесса в будущем, но степень истинности такого прогноза в значительной мере обусловливается аргументированностью выбора пределов экстраполяции и стабиль­ностью измерений. Так же следует обратить внимание на то, что слож­ные объекты, как правило, не могут быть охарактеризованы одним параметром.

Основные этапы действий при статистическом анализе тенден­ций и экстраполяции:

.- во-первых, сбор и систематизация данных. Сбор исходной информации о значении исследуемой характеристики. Проверка однородности дан­ных и их сопоставимость. При необходимости предварительная обработка исходной информации: усреднение значений временного ряда (сглаживание данных). Построение временной характеристики;

.- во-вторых, выбор функции экстраполяции и расчет параметров выбранной функции. В зависимости от того, какая функция будет выбрана, будет зависеть точность выполненного прогноза.

.- в-третьих, расчет границ доверительного интервала прогноза.

Использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс  представляет собой сочетание двух составляющих: регулярной составляющей  и случайной переменной . Временной ряд может условно представлен в виде:

Регулярная составляющая называется трендом (или тенденцией) и характеризует существующую динамику развития процесса в целом. Случайная составляющая отражает случайные колебания (шумы процесса).

При разработке моделей прогнозирования тренд является основной составляющей прогнозируемого времен­ного ряда, на которую уже накладываются другие составляющие. Ре­зультат при этом связывается исключительно с ходом времени. Пред­полагается, что через время можно выразить влияние всех основ­ных факторов.

Выделение тенденции в массиве данных сводится к определению среднего значения за выбранный период. При этом среднее значение может определяться в виде:

- Среднее арифметическое значение

- Взвешенное среднее арифметическое значение

- Среднее экспоненциальное значение

Средние скользящие значения обычно используются для сглаживания краткосрочных колебаний и выделения основных тенденций или циклов, тем самым позволяя увидеть скрытые тренды в рассматриваемых данных. Тренд характеризует процесс изменения показателя за длительное время, исключая случайные колебания.

Среднее арифметическое значение (Simple Moving Average, SMA) определяется как сумма чисел за рассматриваемый период, которую разделили на количество этих чисел за период.

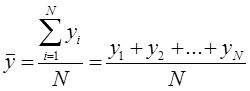
 - значение функции (значение случайной величины) в i-точке;

- период расчета (целое положительное число);

- среднее арифметическое значение за рассматриваемый период N.

Взвешенное среднее арифметическое значение (Weighted Moving Average, WMA) применяется, когда к каждому известному значению  можно присвоить отдельные значения веса .

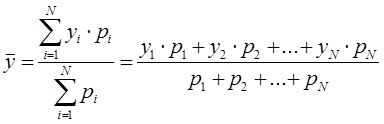
 - значение функции (значение случайной величины) в i-точке;

 - вес известного значения;

- период расчета (целое положительное число);

- взвешенное среднее арифметическое значение за рассматриваемый период N.

 

Экспоненциальное среднее значение (Exponential Moving Average, EMA) является частным случаем взвешенного скользящего среднего, когда значение веса  убывает экспоненциально и никогда не равно нулю. Среднее экспоненциальное значение определяется следующей формулой:

- среднее экспоненциальное значение в i-точке

-   значение функции (значение случайной величины) в i-точке

- сглаживающая константа, коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.

При этом, в качестве первого значения берется простое скользящее среднее (Simple Moving Average) с тем же самым интервалом сглаживания. экспоненциального скользящего среднего.

Коэффициент , может быть выбран произвольным образом, в пределах от 0 до 1. Однако в практике технического анализа на реальном рынке такой подход не применим, поскольку статистический ряд постоянно дополняется новыми значениями цен. Это делает невозможным одновременно зафиксировать α коэффициент и соблюсти критерий минимизации среднеквадратической ошибки. С этой целью для расчета α коэффициента используется следующая формула:

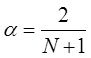
- период расчета (целое положительное число) или интервал сглаживания.

Измеренные значения  находятся в диапазоне (интервале) относительно рассчитанного среднего значения. Диапазон измерений обозначается буквой греческого алфавита - сигма .

- среднее значение за рассматриваемый период N;

- отклонение от среднего значения.

Аналитический расчет диапазона (интервала) измерений может быть выполнен по формуле определения среднеквадратичного отклонения.

Среднеквадратичное (стандартное) отклонение - показывает среднее значение разброса измеренной величины относительно среднего значения. Оценка среднеквадратичного (стандартного) отклонения может быть выполнена по формуле:

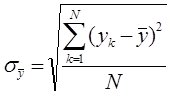
- период расчета (целое положительное число);

- среднее арифметическое значение за рассматриваемый период N;

Cреднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения. Следует заметить, что с вероятностью 0,9973 (99,73%) значение нормально распределённой случайной величины лежит в интервале ., другими словами значения распределённой случайной величины лежат в диапазоне:

Методы экстраполяции

Далее в статье рассмотрены основные методы экстраполяции данных. Следует отметить, что ни один из существующих методов не может обеспечить достаточной точности прогнозов. Применяе­мый в прогнозировании метод экстраполяции не дает точных резуль­татов на длительный срок прогноза, потому что данный метод исхо­дит из прошлого и настоящего, и тем самым погрешность накапли­вается. Этот метод дает положительные результаты на ближайшую (краткосрочную) перспективу прогнозирования тех или иных объектов.

Ниже представленные методы экстраполяции, которые позволяют определить параметры функции на основе ранее полученных данных (точки из заданной выборки). Вначале рассматривается способ построения интерполяционного полинома через (непосредственно) точки заданной выборки. В последствии в статье рассматривается способ построения интерполяционного полинома (однофакторные и многофакторные функции) в непосредственной близости от точек из заданной выборки.

П1. Экстраполяция на основе интерполяционного полиномома n-степени.

 

Интерполяционный полином n-степени – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.

В общем виде интерполяционный многочлен записывается следующим образом:

Для получения интерполяционного многочлена, который будет соединять все заданные точки из набора значений, используют либо построение через форму Лагранжа, либо  построение через форму Ньютона.

Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.

В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде:

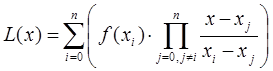
где  ˗ степень полинома ;

 ˗  значение значения интерполирующей функции  в точке ;

 ˗  базисные полиномы (множитель Лагранжа), которые определяются по формуле:

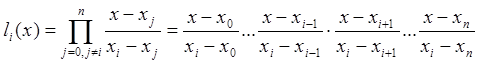
Интерполяционный многочлен в форме Ньютона – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки с постоянным временным шагом измерений.

В общем виде интерполяционный многочлен в форме Ньютона записывается в следующем виде:

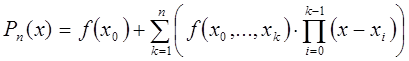
где n – вещественное число, которое указывает степень полинома;

 –  переменная, которая представляет собой разделенную разность k-го порядка, которая вычисляется по следующей формуле:

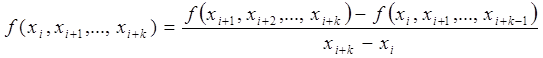
Разделённая разность является симметричной функцией своих аргументов, то есть при любой их перестановке её значение не меняется. Следует отметить, что для разделённой разности k-го порядка справедлива следующая формула:

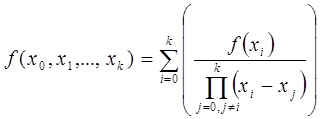
Недостатки метода интерполяции данных на основе интерполяционного полиномома n-степени:

П1. С ростом числа точек порядок многочлена возрастает, а вместе с ним возрастает число операций, которое нужно выполнить для вычисления точки на кривой.

П2. С ростом числа точек у интерполяционной кривой могут возникнуть осцилляции, когда построенный интерполяционный многочлен в промежуточных точках кривой будет очень сильно (нехарактерно) раскачиваться и далеко уходить от заданных точек.

П3. С ростом числа точек плохо подходит для экстраполяции, так как значение многочлена степени n>0 вне отрезка интерполяции всегда расходится к бесконечности (тем быстрее, чем больше n) вне зависимости от сходимости экстраполируемой функции.

П2. Экстраполяция на основе однофакторной функции

Однофакторные функции - это такие функции, в которых прогнозируемый показатель зависит только от одной переменной (одного признака). В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Однако вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а действие многочисленных влияющих на него факторов, которые сложно выделить и определить.

В качестве однофакторных функций используются следующие функции, в которых временная переменная обозначена символом t (фактор-аргумент).

П.1. Степенной полином

Степенной полином может описать любые процессы изменения показателя в зависимости от значений времени. Корреляционное отношение для степенного полинома, служащее мерой тесноты корреляционной связи в нелинейных моделях, приближается к единице по мере увеличения числа степеней полинома до числа уровней временного ряда. Одновременно линия регрессии приближается к фактическим уровням показателя за прошедшее время, что не позволяет установить его тренд и экстраполировать его на перспективу. Поэтому для прогнозирования обычно не применяют полином выше третьей степени. Таким образом, в качестве прогнозирующей функции целесообразно использовать лишь три частных случая степенного полинома: линейную модель, параболу и полином третьего порядка.

П.1.1. Линейная функция (частный случай полинома)

Однофакторная линейная модель отражает постоянный ежегодный абсолютный прирост, т.е. арифметическую прогрессию.

П.1.2. Парабола (частный случай полинома)

Парабола (степенной полином) второго порядка описывает случаи увеличения абсолютного ежегодного прироста на постоянную величину, а третьего порядка – кривую с двумя точками изгибов.

П.2. Экспоненциальная (показательная) функция

Экспонента первого порядка (показательная функция) предусматривает постоянный ежегодный темп роста, равный  процентов (т.е. геометрическую прогрессию), а второго порядка – постоянное увеличение ежегодных темпов роста враз.

П.3. Степенная функция

Степенная функция соответствует случаю ускоряющегося при а1>1 или замедляющегося при а1<1 роста абсолютного ежегодного прироста.

П.4. Логарифмическая функция

Логарифмическая функция выражает случай сокращения абсолютного ежегодного прироста, а функции Торнквиста и Конюса, комбинация линейной функции с логарифмической – затухающий рост абсолютного ежегодного прироста. Логистическая (сигмоидальная) кривая представляет собой модифицированную геометрическую прогрессию, в которой возрастание затухает по мере приближения к определенному пределу.

П.4.1. Комбинация линейной и логарифмической функций

П.4.2. Функция Конюса

П.4.3. Функция Торнквиста

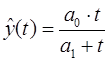
П.4.4. Функция логистическая (сигмоидальная)

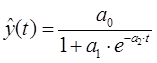
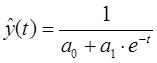
П.5. Гиперболическая функция (Гипербола)

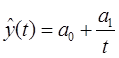
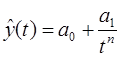
Гиперболическая функция характерна для тех случаев, когда в начальной стадии абсолютные уровни показателя резко сокращаются, а на последующих этапах этот процесс сокращения постепенно затухает

П.5.1. Комбинация линейной функции и гиперболы

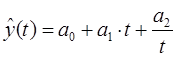
П.6. При прогнозировании колебательных (циклических) процессов применяют тригонометрические функции, ряды Фурье.

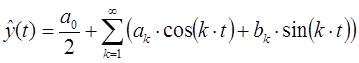
k – количество учитываемых гармоник в сигнале.

Прогнозирование данных в будущем обеспечивают с помощью выбора функции, которая наилучшем образом описывает изменение наблюдаемой величины в прошлом. Для выбранной функции определяют значения коэффициентов выбранной функции. Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпиричес­ким значениям применяется метод наименьших квадратов. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи.

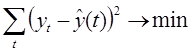
где  – значение выбранной однофакторной функции в заданной точке, - исследуемый временной ряд в заданной точке

Полученное выражение носит название целевой функции. Целевая функция – эта функция нескольких переменных, подлежащая оптимизации (минимизации или максимизации) в целях решения некоторой оптимизационной задачи.

С помощью метода наименьших квадратов могут быть определены неизвестные коэффициенты во всех однофакторных прогнозирующих функциях.

В качестве примера, рассмотрим однофакторную функцию вида «линейная функция», с помощью которой будем моделировать заданный временной ряд.

Поиск неизвестных коэффициентов  осуществляется с помощью метода наименьших квадратов. В соответствии с методом наименьших квадратов запишем целевую функцию:

 

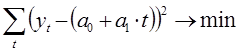
Целевая функция имеет минимум там, где частная производная по неизвестным коэффициентам равна нулю.  В результате у нас выражение перепишется в следующую систему уравнений:

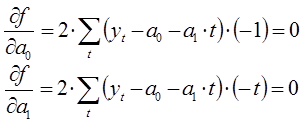
Преобразуем полученную систему уравнений: для системы уравнений проведены сокращения, раскрытие скобок, перенос известных величин вправо, а неизвестных влево. В результате получим следующую систему уравнений:

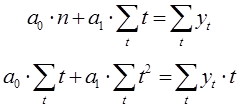
n – количество используемых измерений в заданном временном ряду.

Из полученной системы уравнений определим неизвестные коэффициенты  следующим образом:

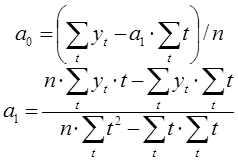
Таким образом, определив неизвестные коэффициенты  можно построить однофакторную функцию на заданном отрезке времени и сделать прогноз изменения функции в будущем.

 

П3. Экстраполяция на основе многофакторных прогнозирующих функций

Многофакторные зависимости определяются поведением не одного параметра, а многих факторов одновременно. Чтобы построить такую модель, вначале необходимо определить факторы, которые оказывают наибольшее влияние на исходные данные.

Многофакторные модели могут быть как линейными, так и нелинейными. 

П.1. в виде линейной многофакторной модели:

где – неизвестные коэффициенты модели,

– аргументы, влияющие на прогнозируемый показатель

П.2. в виде нелинейной многофакторной модели (степенного типа), которая может быть преобразована в линейную модель с помощью логарифмирования:

Более сложные виды нелинейных многофакторных моделей редко используются в практике прогнозирования и планирования.

Неизвестные коэффициенты выражений  определяются с помощью метода наименьших квадратов из системы нормальных уравнений. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи.

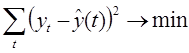
Целевая функция имеет минимум там, где частная производная по неизвестным коэффициентам   равна нулю.  В результате у нас выражение перепишется в следующую систему уравнений:

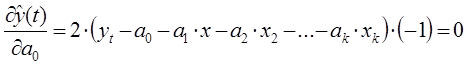
В результате решения данной системы уравнений определяются неизвестные коэффициентам   при которых полученная система уравнений стремится к нулю.

Факторы-аргументы должны отвечать следующим условиям:

во-первых, иметь количественное измерение и отражаться в отчетах или, по крайней мере, определяться на основе специального анализа отчетных данных;

во-вторых, иметь перспективные оценки значений на прогнозируемый период;

в-третьих, число включаемых в модель факторов должно быть меньше числа данных ряда в три раза;

в-четвертых, быть линейно независимыми.

 

 П4. Экстраполяция на основе нейронной сети

Искусственные нейронные сети широко используются в задачах экстраполяции данных, когда неизвестен точный вид связи (функции) между входными и выходными значениями. Нейронная сеть является сложной нелинейной системой с огромным числом степеней свободы, что позволяет ей подстраивается под любые начальные данные.

Искусственная нейронная сеть состоит из искусственных нейронов. Структурная схема искусственного нейрона приведена ниже.

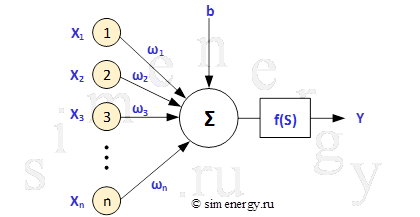
Рис.2. Структурная схема искусственного нейрона

Искусственный нейрон имеет несколько входных сигналов (несколько входов) и только один выходной (единственный выход). Каждый вход имеет некоторый вес, на который умножается значение, поступившее по данному входу. В теле (ячейке) нейрона происходит суммирование взвешенных входов в соответствии с формулой:

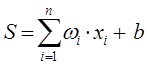
 n — размерность входного вектора

— вес i-го входа нейрон

 — значение, поступающее на i-й вход нейрона

Как уже было написано, в теле нейрона происходит суммирование взвешенных входов, а полученная сумма преобразуется с помощью активационной (передаточной) функции нейрона (обычно нелинейной) в выходное значение нейрона.  Полученная сумма поступает в качестве аргумента S на функцию активации , результат которой является выходным значением нейрона.

Активационная функция (передаточная функция) может иметь различный вид: бинарный, пороговый, линейный, сигмоидальный. Одной из наиболее распространенных видов активационной функции является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

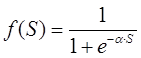
При уменьшении α сигмоид становится более пологим, в пределе при α=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении α сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. 

Нейроны соединены между собой с помощью синапсов - упрощенных аналогов синаптических контактов нервных клеток, обладающих способностью изменять и сохранять свой вес (величину). Целенаправленная перестройка весов синапсов (т.е. коэффициентов, на которые умножаются входные сигналы, или подстроечных параметров) позволяет нейрону избирательно реагировать на сигналы других нейронов, обеспечивая на выходе наиболее “полезные” сигналы.

Если нейронная сеть имеет дополнительные слои между входным и выходным слоем, то они называются скрытыми, а обучение такой сети - глубоким. Дополнительные скрытые слои могут помочь нейросети определить более сложные закономерности между входными и желаемыми выходными данными.

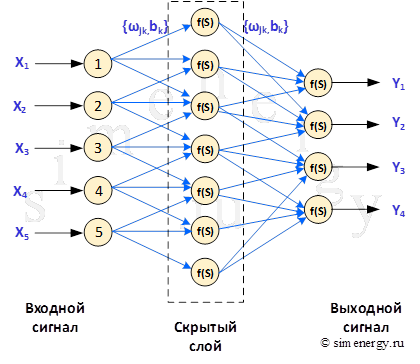
Рис.3. Структурная схема нейронной сети

После создания структуры нейронной сети выполняется процесс обучения нейронной сети. В процессе обучения происходит подбор коэффициентов нейронной сети  тем самым выстраивается зависимость между заранее известными входными и выходными данными. Обучение нейронной сети означает, что для заданного набора заранее известных входных и выходных данных, необходимо подобрать оптимальные коэффициенты  нейросети так, что квадратичная ошибка между точным выходным значением и выходным значением, полученным посредством распространения входных значений через нейронную сеть, стремилась к минимуму:

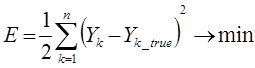
Поиск оптимальных коэффициентов производится методом градиентного спуска с использованием метода обратного распространения ошибки.

 

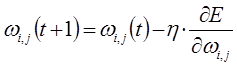
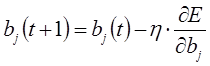
Производные функции минимизации определяются по следующим формулам:

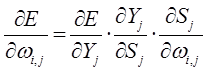
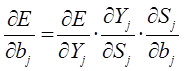
В представленной системе уравнений частные производные имеют следующий вид:

 

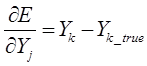
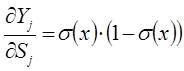
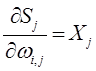
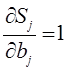
В настоящее время для создания и обучения нейронных сетей используют программные комплексы с готовыми библиотеками, например, на базе языка программирования Python.

Таким образом, экстраполяцию можно использовать в качестве средства для определения будущих, ожидаемых значений величин, на основе имеющихся данных о тенденциях их изменений в прошлые периоды. С оптимальным выбором метода экстраполяции возможно получить максимально точный результат, который будет правильно отражать будущие значения.