› Формула Тейлора для функции одной переменной
Ряд Тейлора (в англоязычной литературе Taylor series) – это способ представления сложной функции (периодической или непериодической) с помощью бесконечной суммы простейших степенных функций.
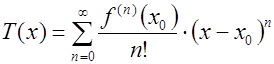
где ![]() - степенной ряд, полученный разложением функции
- степенной ряд, полученный разложением функции ![]() в окрестности точке
в окрестности точке ![]() в ряд Тейлора;
в ряд Тейлора;
![]() – точка, в окрестности которой производится разложение функции
– точка, в окрестности которой производится разложение функции ![]() ;
;
![]() – производная n-степени функции
– производная n-степени функции ![]() в окрестности точке
в окрестности точке ![]()
n – число членов ряда разложения.
Следует отметить, что в случае, если ![]() , то ряд Тейлора преобразуется в ряд Маклорена (в англоязычной литературе Maclaurin series).
, то ряд Тейлора преобразуется в ряд Маклорена (в англоязычной литературе Maclaurin series).
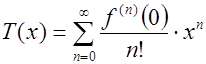
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка. Так же формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении.
› Формула Тейлора для функции двух переменных
В случае если функция ![]() является функцией от двух переменных и имеет производные вплоть до n-го порядка включительно в некоторой окрестности точки
является функцией от двух переменных и имеет производные вплоть до n-го порядка включительно в некоторой окрестности точки ![]() , тогда разложение функции в ряд Тейлора будет иметь следующий вид:
, тогда разложение функции в ряд Тейлора будет иметь следующий вид:
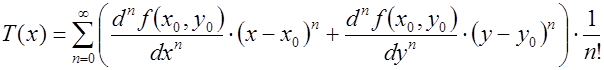
где ![]() - степенной ряд, полученный разложением функции
- степенной ряд, полученный разложением функции ![]() в окрестности точке
в окрестности точке ![]() в ряд Тейлора;
в ряд Тейлора;
n – число членов ряда разложения.
Представленная формула распространяется на функции от любого числа переменных.
В качестве первого примера, рассмотрим разложение тригонометрической функции ![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки ![]() .
.
Рассматриваемая функция ![]() дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом:
дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом: 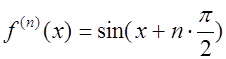 . Таким образом, функция
. Таким образом, функция ![]() раскладывается в следующий ряд Тейлора:
раскладывается в следующий ряд Тейлора:
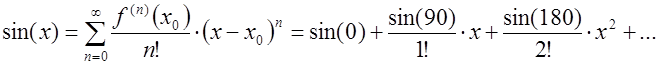
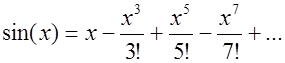
В итоге получаем следующий степенной ряд:
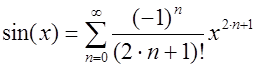
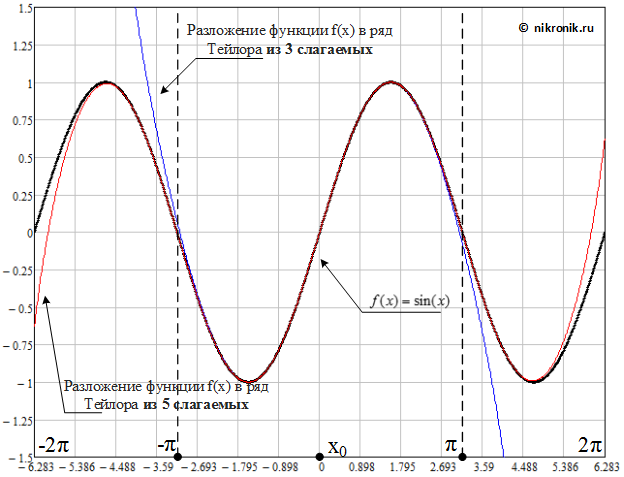
Рис.1. Зависимость изменения функция ![]() и ее представление в виде ряда Тейлора
и ее представление в виде ряда Тейлора
В качестве второго примера, рассмотрим разложение тригонометрической функции ![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки ![]() .
.
Рассматриваемая функция ![]() дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом:
дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом: 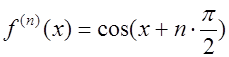 . Таким образом, функция
. Таким образом, функция ![]() раскладывается в следующий ряд Тейлора:
раскладывается в следующий ряд Тейлора:
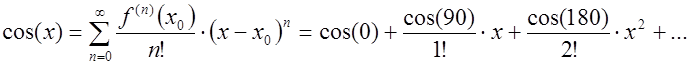
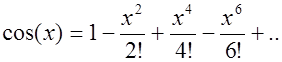
В итоге получаем следующий степенной ряд:
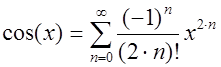
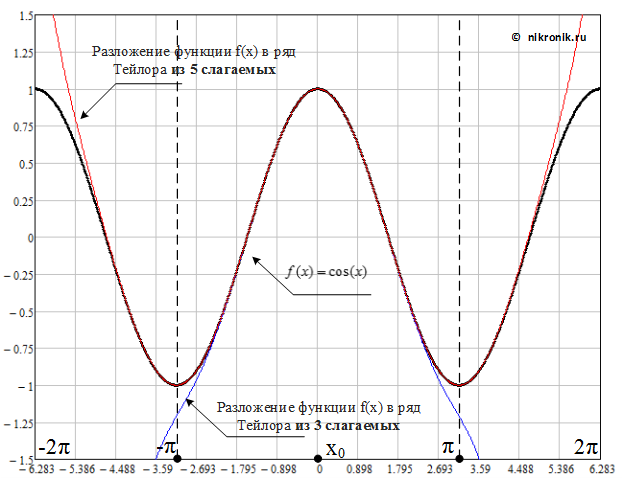
Рис.2. Зависимость изменения функция ![]() и ее представление в виде ряда Тейлора
и ее представление в виде ряда Тейлора
В качестве третьего примера, рассмотрим разложение тригонометрической функции ![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки ![]() .
.
Рассматриваемая функция ![]() дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом:
дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом: 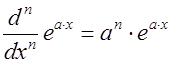 . Таким образом, функция
. Таким образом, функция ![]() раскладывается в следующий ряд Тейлора:
раскладывается в следующий ряд Тейлора:
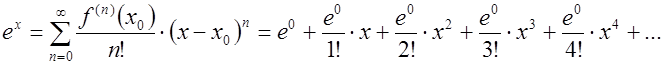
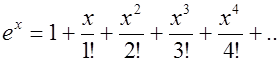
В итоге получаем следующий степенной ряд:
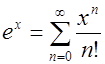
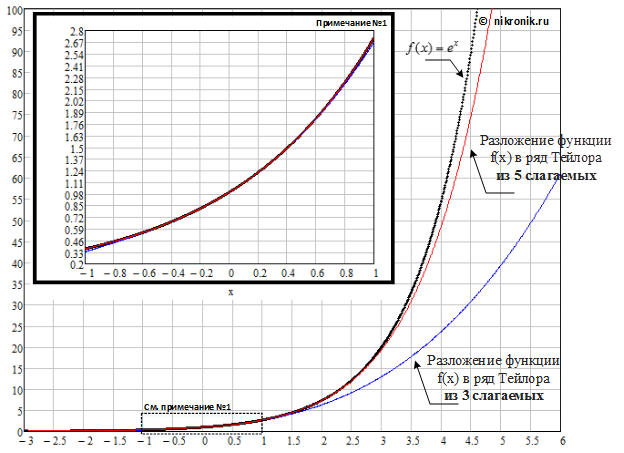
Рис.3. Зависимость изменения функция ![]() и ее представление в виде ряда Тейлора
и ее представление в виде ряда Тейлора