Рассмотрим систему уравнений для напряжений и потокосцеплений статорных контуров:
Установившийся режим работы синхронной машины характеризуется отсутствием токов в демпферных контурах синхронной машины (
,
), отсутствием изменения результирующего магнитного потока (
,
), также сделаем допущение по величине скольжения в установившемся режиме(
).
С учетом описанных допущений система уравнений для напряжений и потокосцеплений статорных контуров перепишется в следующем виде:
При выполнении расчетом совместим вещественную ось с осью q, а мнимую ось с осью d. В результате получим, что напряжение на шинах синхронной машины определяется по формуле: 
, 
.
Введем вспомогательную ЭДС (EQ), которая определяется по следующей формуле:
В результате получаем следующее выражение:
В результате мы получили уравнение, которое описывает процессы, происходящие в эквивалентном генераторе в установившемся режиме работы. Схема замещения синхронной машины, которая отвечает представленному уравнению, выглядит следующим образом:
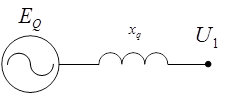
Рис.1. Схема замещения эквивалентного генератора
Схема замещения синхронной машины в установившемся режиме работы представляет собой источник ЭДС (вспомогательная ЭДС - EQ) за реактивным сопротивлением синхронной машины по поперечной оси (xq). При этом следует отметить, что переменная EQ не имеет физического смысла, данная переменная была введена специально, чтобы получить схему замещения синхронной машины в общем виде. Полученная схема замещения соответствует схеме замещения явнополюсной синхронной машины при рассмотрении установившихся режимов работы.
В случае если синхронная машина является неявнополюсной (синхронные индуктивные сопротивления по продольной (xd) и поперечной (xq) оси одинаковы) схема замещения представляет собой источник ЭДС (синхронная ЭДС статора - Eq) за реактивным сопротивлением синхронной машины (xq = xd).
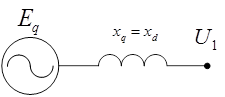
Рис.2. Схема замещения неявнополюсного эквивалентного генератора
Векторная диаграмма синхронной машины в установившемся режиме работы.
Запишем уравнение, которое описывает процессы, происходящие в явнополюсной синхронной машине в установившемся режиме работы. В случае совмещения напряжение на шинах генератора с вещественной осью (
) и с учетом уравнения для мощности 
(о.е.), уравнение для определения EQ перепишется следующим образом:
Примечание: В именованных единицах формулы для определения мощности выглядит следующим образом: 
(и.е.), однако при выводе последующих формул используется формула , которая связывает параметры в относительных единицах. В качестве базисных величин выбраны следующие переменные: линейное напряжение и фазный ток. В результате при переводе формулы из именованных единиц в относительные единицы получим запись: (о.е.).
В векторной форме уравнение для определения EQ определяется в следующем виде:
,
где 
,
,
,
.
Для упрощения окончательной записи и облегчения построения векторной диаграммы синхронной машины пренебрежем активным сопротивлением статорной обмотки. В результате получим:
, 
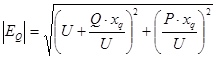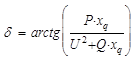
I. Построим для установившегося режима работы векторную диаграмму синхронной машины в режим перевозбуждения (синхронная машина выдаем в сеть реактивную мощность).
1. Построение векторной диаграммы начинается с построение векторов U и I по заданным значениям активной (P>0) и реактивной (Q>0) мощности, а также заданного напряжения.
2. Вычисление и построение вектора EQ, а также осей q и d.
3. Построение переменных 
, 
, 
и 
.
4. Вычисление и построение векторов Eq, E’q и E’’q.
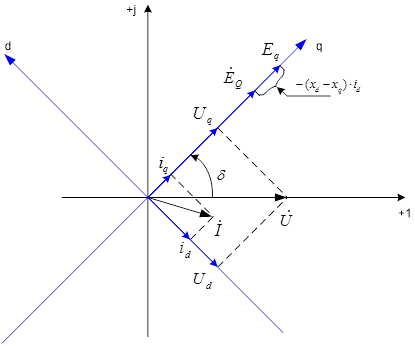
Рис.3. Векторная диаграмма синхронной машины в режиме перевозбуждения
II. Построим для установившегося режима работы векторную диаграмму синхронной машины в режим недовозбуждения (синхронная машина потребляет реактивную мощность из сети).
1. Построение векторной диаграммы начинается с построение векторов 
и 
по заданным значениям активной (P>0) и реактивной (Q<0) мощности, а также заданного напряжения.
2. Вычисление и построение вектора EQ, а также осей q и d.
3. Построение переменных , , и .
4. Вычисление и построение векторов Eq, E’q и E’’q.
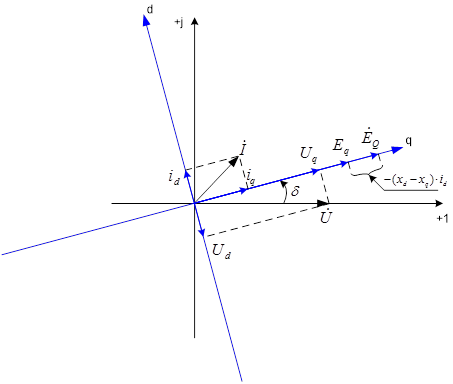
Рис.4. Векторная диаграмма синхронной машины в режиме недовозбуждения.
В качестве примера, определим необходимые параметры явнополюсного синхронного генератора и построить векторную диаграмму при условии, что генератор работает в режиме номинальной мощности 
(о.е.), 
, напряжение на шинах составляет 
(о.е.) и 
(о.е.).
Решение:
(о.е.)
(о.е.)
, 
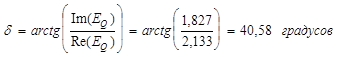
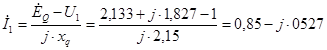(о.е.)
; 
, 
(о.е.)
; 
; 
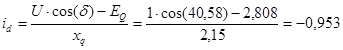
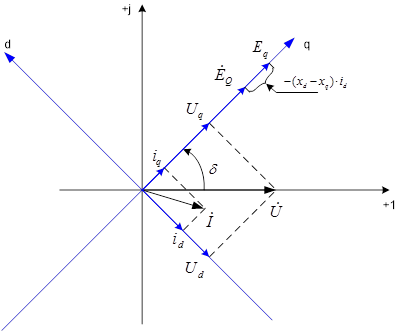
Рис.5. Векторная диаграмма синхронной машины в режиме перевозбуждения
