Режим работы электроэнергетической системы в любой момент времени характеризуется изменяющимися мгновенными значениями тока и напряжения. Для оценки текущего режима работы устройства релейной защиты и автоматики оцифровывают мгновенные значения в последовательность дискретных значений, замеренных одновременно в равноотстоящие моменты времени. Таким образом, непрерывный аналоговый сигнал становится дискретной последовательностью цифрового сигнала.

Рис. 1. Изменение дискретного сигнала на временном интервале
Полученный дискретный сигнал в общем случае может состоять из бесконечной суммы гармонических колебаний различной частоты. Разложение исходной дискретной функции, которая определена N-точками измерений на заданном временном интервале, к функции, которая определена на частотном диапазоне, осуществляется с помощью прямого дискретного преобразования Фурье.
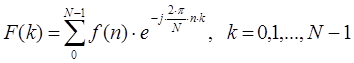
N ˗ количество значений сигнала, измеренных за период, а также кратность частотного спектра;
k ˗ индекс кратности частоты.
Однако переходные процессы в электроэнергетических системах в большинстве случаев описываются гармонической функцией с периодом колебания равной основной частоте (частоте сети), которая в свою очередь может меняться в зависимости от характера переходных процессов. В электроэнергетике генерирующее оборудование, работающее синхронно с энергосистемой, участвует в процессе поддержания частоты переменного тока в энергосистеме в допустимых пределах (50,00±0,2 Гц,). Поэтому в большинстве случаев установившийся или аварийный (короткое замыкание) режим работы электроэнергетической системы в любой момент времени характеризуется изменением мгновенных значений тока и напряжения с номинальной частотой сети или близкой к номинальной частоте сети.
Примечание: В нормальном режиме частота может меняется в диапазоне - 50,00±0,05 Гц, а в аварийных режимах работы при выделении энергорайонов на изолированную работу с дефицитом/избытком генерирующей мощности частота может снижаться/повышаться до частоты 45/55 Гц, соответственно.
Прямое дискретное преобразование Фурье с учетом формулы Эйлера позволяет определить не зависящую от времени постоянную составляющую (амплитуду постоянной составляющей сигнала) и составляющую гармонического колебания основной частоты (амплитуду и фазу первой гармоники сигнала).
Постоянная составляющая (k=0) сигнала определяется следующим выражением внутри диапазона от 0 до 2π:
![]()
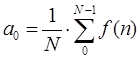
Гармоническое колебание основной частоты (k=1) определяется следующим выражением внутри диапазона от 0 до 2π:
![]()
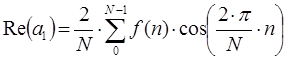
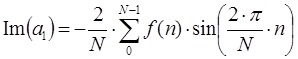
Следует отметить, что вместо экспоненты мнимого аргумента можно пользоваться представлением через синус и косинус, тогда периодический сигнал может быть представлен следующим образом:
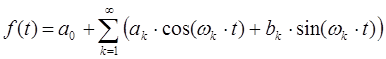
где коэффициенты ![]() ,
, ![]() и
и ![]() называются коэффициентами Фурье. Однако векторное (комплексное) представление аналогового сигнала упрощает запись, а также совершаемые математические операции над функциями, т.к. методы определения большинства режимных параметров широко известны и базируются на использовании комплексных значений токов и напряжений.
называются коэффициентами Фурье. Однако векторное (комплексное) представление аналогового сигнала упрощает запись, а также совершаемые математические операции над функциями, т.к. методы определения большинства режимных параметров широко известны и базируются на использовании комплексных значений токов и напряжений.
Комплексное число может быть записано в алгебраической, тригонометрической и показательной форме следующим образом:
![]()
![]() – это модуль комплексного числа (амплитуда вектора),
– это модуль комплексного числа (амплитуда вектора),
![]()
![]() – аргумент комплексного числа (начальная фаза).
– аргумент комплексного числа (начальная фаза).
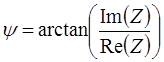
С помощью представленных соотношений определяются комплексные величины напряжения и тока в каждой фазе. Остальные электрические величины определяются по известным формулам, которые связывают полученные комплексные значения тока и напряжения.
Комплексное сопротивление определяется отношением напряжения на элементе к току, который протекает в элементе.
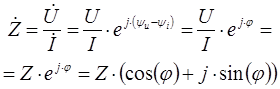
![]() - комплексная величина действующего фазного напряжения;
- комплексная величина действующего фазного напряжения;
![]() - комплексная величина действующего тока, который протекает в фазе.
- комплексная величина действующего тока, который протекает в фазе.
Комплексная мощность определяется произведением комплексного напряжения на сопряженную величину комплексного тока.
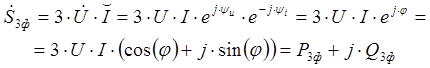
![]() - комплексная величина действующего фазного напряжения;
- комплексная величина действующего фазного напряжения;
![]() - сопряженная комплексная величина действующего тока, который протекает в фазе.
- сопряженная комплексная величина действующего тока, который протекает в фазе.
Для отображения полученных векторов электрических величин (тока, напряжения, сопротивления и мощности) используют векторную диаграмму. В основном векторные диаграммы изображают для действующих значений (I = Im /√2), а не амплитудных (Im). Использование векторных диаграмм при анализе переходных процессов позволяет доступно и наглядно рассмотреть происходящие процессы, а также дает отчетливое представление о характере процесса (опережение/отставание различных электрических величин друг от друга).
Методика расчета.
Рассмотрим методику перехода от мгновенного значения переменной (тока или напряжения) к векторной переменной для дальнейшей цифровой обработки данных.
1 шаг: Определяется период расчета для расчета коэффициентов Фурье (от 0 до 2π). Для этого по данным дискретного сигнала на каждом шаге расчета определяется значение текущей частоты исходного сигнала (в зависимости от характера переходных процессов частота может меняться в диапазоне 45-55 Гц), а также определяется (вычисляется) количество точек дискретизации за указанный период.
2 шаг: Выполняется расчет коэффициентов Фурье для заданной дискретной функции в соответствии с найденным периодом расчета.
Постоянная составляющая сигнала определяется следующим выражением внутри диапазона от 0 до 2π:
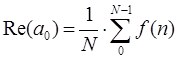
Гармоническое колебание основной частоты (основная гармоника) определяется следующим выражением внутри диапазона от 0 до 2π:
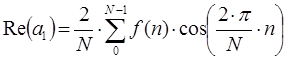
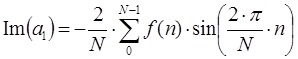
3 шаг: В следующий момент времени окно смещается на следующую точку данных дискретного сигнала и возвращаемся к шагу №1. Расчет коэффициентов Фурье выполняется для всего диапазона данных дискретного сигнала.
Следует отметить, что в случае анализа переходных процессов, которые вызывают появление в токе или напряжении различных гармонических составляющих, исходный сигнал необходимо раскладывать на весь доступный спектр, для анализа содержания высших гармонических составляющих в рассматриваемом сигнале.