Метод половинного деления (метод также известен как метод Больцано или метод дихотомии) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения 
. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность 
.
Пусть дано уравнение 
и определен отрезок 
такой, что данный отрезок содержит один единственный корень уравнения 
. Тогда по концам заданного отрезка функция имеет значения, противоположные по знаку: 
. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
.
Отрезок 
называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности 
, 
, и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция 
имеет разные знаки.
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
› Рассмотрим алгоритм метода половинного деления.
1. Найти начальный интервал неопределенности 
одним из методов отделения корней, задать малое положительное число . Положить 
.
2. Найти середину текущего интервала неопределенности:
.
3. Необходимо найти значение функции в точках 
, 
и 
. Далее необходимо проверить два условия:
- если выполняется условие 
, то искомый корень находится внутри левого отрезка положить
, 
;
- если выполняется условие 
, то искомый корень находится внутри правого отрезка принять 
, 
.
В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:
.
4. Проверяем новый отрезок на предмет заданной точности, в случае:
- если длина нового отрезка меньше заданной точности 
, то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:
.
- если длина нового отрезка не достигает необходимой точности 
, то необходимо продолжить итерационный процесс 
и перейти к п.2 рассматриваемого алгоритма.
Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза:
Из данного соотношения можно оценить число итераций k для достижения заданной точности :
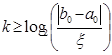
Из полученной формулы можно сделать вывод, что для достижения точности 
от длины первоначального промежутка 
необходимо выполнить примерно десять итераций.
К достоинствам метода также следует отнести то, что он позволяет найти простой корень уравнения 
любых непрерывных функций при любых значениях 
таких, что 
.
Недостатки метода — он не обобщается на системы нелинейных уравнений и не может использоваться для нахождения корней четной кратности.
В качестве примера, рассмотрим решение нелинейного уравнения 
методом половинного деления. Корень необходимо найти в рассматриваемом диапазоне 
с точностью 
.
Вариант решения нелинейного уравнения в программном комплексе MathCAD.
Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага расчета представлены графической форме (см. рис.1).
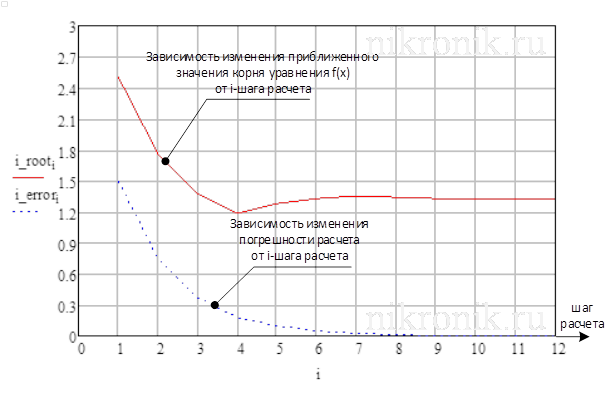
Рис.1. Результаты расчета по методу половинного деления
Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 12 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: 
.
