Оптимальное управление нормальными режимами работы электроэнергетической системы заключается в том, чтобы за рассматриваемый период времени обеспечить надежное электроснабжение потребителя электрической энергии требуемого качества при минимальных возможных эксплуатационных затратах.
Одна из практических задач оптимизации режимов работы электроэнергетической сети является задача определения оптимального режима работы, который характеризуется минимумом потерь активной мощности в сети. Целью данной задачи является определение зависимых и независимых параметров режима (X и Y), которые удовлетворяют системе уравнений установившегося режима работы сети, техническим ограничениям на контролируемые величины и целевая функция оптимизации равна наименьшему значению.
В качестве целевой функции будем использовать выражение, которое определяет минимум потерь активной мощности в сети. Другими словами, необходимо найти оптимальный установившийся режим работы сети, при котором достигается минимум целевой функции:
![]() .
.
Установившийся режим работы сети описывается системой нелинейных уравнений:
![]() ,
,
где Y – вектор заданных независимых переменных; X – вектор неизвестных зависимых переменных; W – вектор-функция, которая может быть представлена системой уравнений узловых напряжений в форме баланса токов или системой уравнений узловых напряжений в форме баланса мощностей.
Число уравнений установившегося режима работы в системе уравнений должно быть равно числу зависимых переменных, тогда система имеет одно решение. В случае если число зависимых переменных больше числа уравнений установившегося режима, тогда это означает, что рассматриваемая система уравнений имеет степень свободы. Наличие степени свободы в системе уравнений установившегося режима определяет существование множества возможных режимов работы сети из допустимых режимов, среди которых можно выбирать наиболее оптимальный режим для рассматриваемой сети.
Рассмотрим методику оптимизации режима работы электроэнергетической сети с помощью метода приведенного градиента. Поиск оптимального режима работы по методу приведенного градиента является итерационной процедурой, где вектор столбец неизвестных зависимых переменных определяется на каждом шаге расчета по следующему выражению:
![]()
где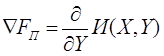 - приведённый градиент функции;
- приведённый градиент функции;
![]() - шаг расчета по методу приведенного градиента.
- шаг расчета по методу приведенного градиента.
Приведённый градиент функции ![]() является проекцией градиента
является проекцией градиента ![]() на плоскость, которая является касательной к нелинейной поверхности, описываемой уравнениями установившийся режим работы сети
на плоскость, которая является касательной к нелинейной поверхности, описываемой уравнениями установившийся режим работы сети ![]() .
.
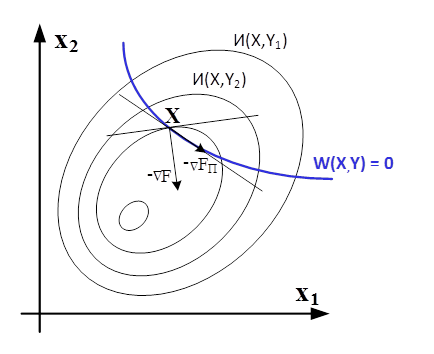
Рис.1. Графическое изображение градиента и приведенного градиента функции
Примечание: градиентные методы являются вычислительными методами решения задач вогнутого программирования для поиска экстремума функции. Градиент ![]() и антиградиент
и антиградиент ![]() ортогонален поверхности функции
ортогонален поверхности функции ![]() в точке X. Идея градиентных методов основана на том, что антиградиент функции
в точке X. Идея градиентных методов основана на том, что антиградиент функции ![]() указывает направление наиболее быстрого ее убывания в окрестности точки
указывает направление наиболее быстрого ее убывания в окрестности точки ![]() , в которой он вычислен. Поэтому, если из некоторой текущей точки
, в которой он вычислен. Поэтому, если из некоторой текущей точки ![]() перемещаться в направлении антиградиента функции
перемещаться в направлении антиградиента функции ![]() , то функция
, то функция ![]() будет убывать.
будет убывать.
Приведенный градиент функции ![]() определяется через производную целевой функции по независимым переменным. Однако зависимые переменные, которые входят в целевую функцию, являются неявной функцией от независимых переменных, которые определяются уравнениями установившегося режима работы. Поэтому производная целевой функции записывается по правилу вычисления производной с учетом неявных функций:
определяется через производную целевой функции по независимым переменным. Однако зависимые переменные, которые входят в целевую функцию, являются неявной функцией от независимых переменных, которые определяются уравнениями установившегося режима работы. Поэтому производная целевой функции записывается по правилу вычисления производной с учетом неявных функций:
![]()
![]() - вектор-строка размерностью [1 x n], которая определяется из явной зависимости переменных в целевой функции:
- вектор-строка размерностью [1 x n], которая определяется из явной зависимости переменных в целевой функции:
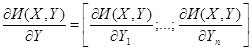
![]() - вектор-строка размерностью [1 x m], которая определяется из явной зависимости переменных в целевой функции:
- вектор-строка размерностью [1 x m], которая определяется из явной зависимости переменных в целевой функции:
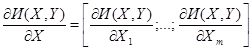
![]() - прямоугольная матрица размерностью [m x n], которая определяется из системы уравнений установившегося режима работы сети
- прямоугольная матрица размерностью [m x n], которая определяется из системы уравнений установившегося режима работы сети ![]() :
:
![]()
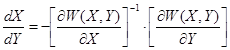
![]() - квадратная матрица размерностью [m x m] (якобиан уравнений установившегося режима):
- квадратная матрица размерностью [m x m] (якобиан уравнений установившегося режима):
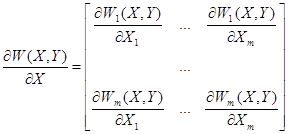
![]() - прямоугольная матрица размерностью [m x n], которая формируется из частных производных системы уравнений установившегося режима по независимым переменным:
- прямоугольная матрица размерностью [m x n], которая формируется из частных производных системы уравнений установившегося режима по независимым переменным:
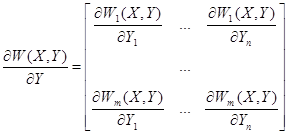
В результате получили выражение для определения приведенного градиента целевой функции.
Следует отметить, что более эффективно с точки зрения вычислений определять приведенный градиент целевой неявной функции по следующему выражению:
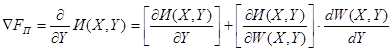
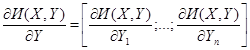 - вектор-строка производных, которая определяется из явной зависимости переменных в целевой функции, размерностью [1 x n]
- вектор-строка производных, которая определяется из явной зависимости переменных в целевой функции, размерностью [1 x n]
![]() - прямоугольная матрица производных системы уравнений установившегося режима по независимым переменным, размерностью [m x n].
- прямоугольная матрица производных системы уравнений установившегося режима по независимым переменным, размерностью [m x n].
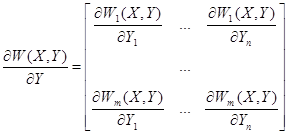
![]() - вектор-строка частных производных минимизируемой функции размерностью [1 x m], которая определяется в результате решения системы линейных уравнений:
- вектор-строка частных производных минимизируемой функции размерностью [1 x m], которая определяется в результате решения системы линейных уравнений:
![]()
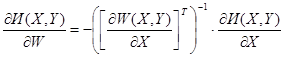
![]() - квадратная матрица частных производных, размерностью [m x m] (якобиан уравнений установившегося режима);
- квадратная матрица частных производных, размерностью [m x m] (якобиан уравнений установившегося режима);
![]() - вектор-столбец размерностью [1 x m]
- вектор-столбец размерностью [1 x m]
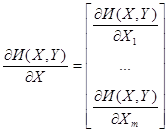
Следует обратить внимание на то, что матрица коэффициентов в этом уравнении является транспонированной матрицей Якоби уравнений установившегося режима.
Рассмотрим методику расчета оптимального режима работы для участка сети, которая состоит из двух узлов и одной ветви. Первый узел является базисно-балансирующим узлом, а во втором узле расположена нагрузка величиной ![]() , а также подключен источник реактивной мощности
, а также подключен источник реактивной мощности ![]() . Необходимо найти значение напряжения в узле 2, а также величину мощности компенсирующего устройства, чтобы потери в рассматриваемой схеме были минимальными.
. Необходимо найти значение напряжения в узле 2, а также величину мощности компенсирующего устройства, чтобы потери в рассматриваемой схеме были минимальными.
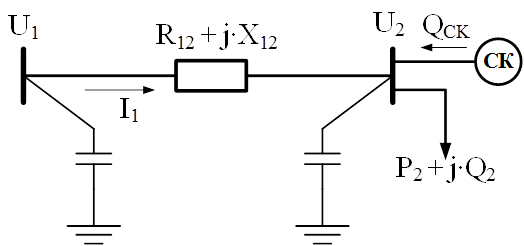
Рис.2. Рассматриваемая схема замещения
Установившийся режим работы описывается системой уравнений узловых напряжений (выражение записано для линейных напряжений):
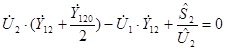
где ![]()
![]() - сопряженное значение мощности и напряжения во втором узле.
- сопряженное значение мощности и напряжения во втором узле.
Данная система уравнений может быть переписана в форме баланса мощностей:
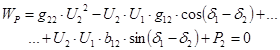
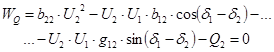
Потери активной мощности в сети определяются по следующей формуле (выражение записано для линейных напряжений):
![]()
где мощности в начале и в конце линии определяются следующим образом:
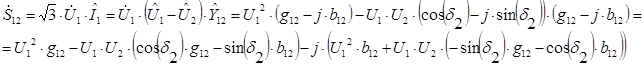
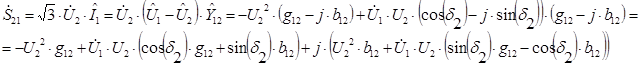
Рассмотрим методику расчета оптимального режима работы при условии минимума потерь в расчетной схеме.
Зависимыми переменными (X) в данном примере является собственный угол напряжения во втором узле ![]()
Независимыми переменными (Y) в данном примере является напряжение во втором узле ![]()
П.1. Определить базисно-балансирующий узел для формирования исходной системы уравнений. По условиям задачи первый узел является базисно-балансирующим узлом, в котором задано напряжение, а также мощность в данном узле определяется из условия обеспечения баланса мощности в расчетной схеме.
П.2. Задать начальное приближение напряжения в узле №2 ![]() , величина которого будет оптимизироваться для обеспечения минимума потерь активной мощности в расчетной схеме.
, величина которого будет оптимизироваться для обеспечения минимума потерь активной мощности в расчетной схеме.
П.3. Записать систему уравнений установившегося режима работы расчетной схемы с учетом принятых начальных данных. В данном случае система уравнений будет состоять из одного уравнения, которое описывает баланс мощности для узла №2.
![]()
Решение данного уравнения выполняется с помощью метода Ньютона в соответствии со следующей итерационной формулой:
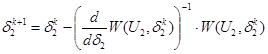
П.4. Определяем потери активной мощности в расчетной схеме на текущем шаге итерации.
![]()
П.5. Определяем прямоугольную матрицу в результате решения системы линейных алгебраических уравнений
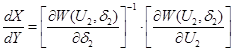
или
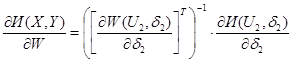
П.6. Определяем приведенный градиент минимизируемой функции по выражению:
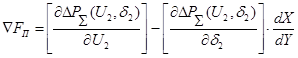
или
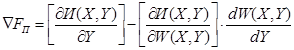
П.7. Определяем новое значение оптимизируемой переменной ![]() в соответствии с выражением:
в соответствии с выражением:
![]()
Возвращаемся к П.2 и повторяем итерационный расчет оптимального режима работы рассматриваемой сети. Итерационный процесс расчета прекращается, когда выполняется следующее условие:
![]()
П.8. Величину мощности компенсирующего устройства, установленного в узле №2, определяют из условия баланса реактивной мощности в узле №2 по выражению:
![]()
Таким образом, расчет оптимального режима состоит в определении значений зависимых и независимых параметров режима, при которых удовлетворяются уравнения установившегося режима, технические ограничения на контролируемые величины и целевая функция оптимизации равна наименьшему значению.