Линия электропередачи (ЛЭП) — один из компонентов электрической сети, система энергетического оборудования, предназначенная для передачи электроэнергии посредством электрического тока. Различают воздушные линии электропередачи и кабельные линии электропередачи.
Любая линия электропередачи является элементом с распределенными параметрами, каждый участок которой характеризуется продольными активно-индуктивными элементами (
и 
), междуфазными взаимными индуктивностями 
, поперечными активно-емкостными элементами (
и 
) и междуфазными емкостными элементами 
(см. рис. 1).
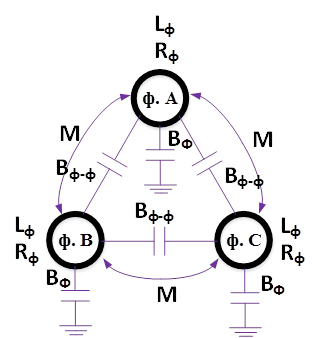
Рис.1. Разрез линии электропередачи с отображением продольных и поперечных элементов
В случае если пространственной протяженностью объекта можно пренебречь, то исследование процессов в таких объектах осуществляется с помощью классических моделей со сосредоточенными параметрами. Такие элементы электрической сети описываются обыкновенными дифференциальными уравнениями, в которых независимой переменной является только время процесса.
Линия электропередачи длинной менее 300 км может быть представлена в виде П-образной схемы замещения, которая состоит из сосредоточенных элементов электрической сети. Параметры такой схемы замещения определяются произведением погонных параметров линии на ее длину. Следует отметить, что при необходимости выполнения расчета многочастотных переходных процессов создается цепочечная схема замещения линии электропередачи из П-образных схем замещения.
Рис.2. П-образная схема замещения трехфазной ЛЭП
Как видно схема замещения в фазной системе координат состоит из двух отдельных частей: первая часть отражает взаимодействие только магнитных полей (активно-индуктивная часть схемы замещения), а вторая часть расчетной схемы отражает электростатическое поле (активно-емкостная часть схемы замещения).
Рассмотрим активно-индуктивную часть схемы замещения линии электропередачи.
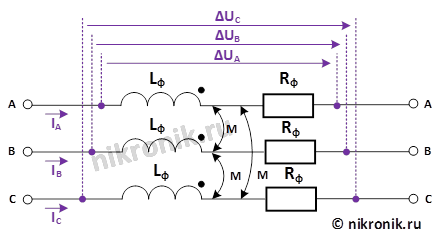
Рис.3. Активно-индуктивная часть схемы замещения трехфазной ЛЭП
Запишем систему уравнений, которая описывает процессы, происходящие в рассматриваемой части схемы замещения транспонированной линии электропередачи (первой участок полной схемы замещения):
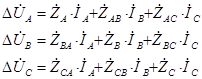
где 
- собственные комплексные сопротивление линии электропередачи, а 
- взаимные комплексные сопротивления линии электропередачи.
Рассмотрим активно-емкостную часть схемы замещения линии электропередачи.
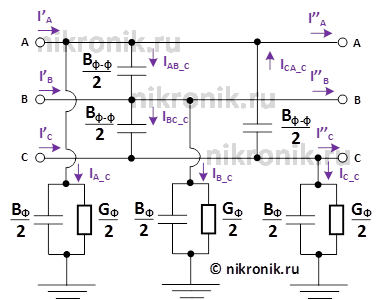
Рис.4. Активно-емкостная часть схемы замещения трехфазной ЛЭП
Запишем систему уравнений, которая описывает процессы, происходящие в рассматриваемой схеме замещения транспонированной линии электропередачи (второй участок полной схемы замещения):
∙ По второму закону Кирхгофа запишем следующую систему уравнений:
∙ По первому закону Кирхгофа запишем следующую систему уравнений:
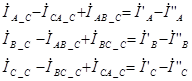
В результате система уравнений, которая описывает процессы, происходящие в рассматриваемой части схемы замещения транспонированной линии электропередачи, записывается в следующем виде:
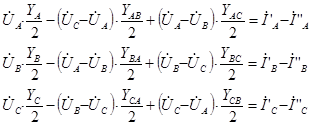
где 
- собственные комплексные проводимости линии электропередачи на землю, а 
- взаимные комплексные проводимости линии электропередачи.
Рассматриваемые системы уравнений содержат сопротивления и емкостные проводимости, которые в общем случае отличаются друг от друга:
и 
и 
Для выравнивания продольных и поперечных сопротивлений и проводимостей выполняют транспозицию фаз на воздушной линии электропередачи. Под транспозицией понимается циклическая перестановка фаз по отношению друг к другу на разных участках линии: провод каждой фазы проходит одну треть длины линии на одном, вторую - на другом и третью - на третьем месте. Такое тройное перемещение проводов называют циклом транспозиции. Шаг транспозиции по условию влияний на линии связи не нормируется. При этом транспозиция должна осуществляться так, чтобы суммарные длины участков ВЛ с различным чередованием фаз были примерно равны.
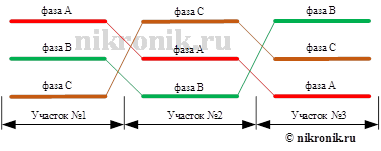
Рис.5. Полный цикл транспозиции фаз воздушной линии
Рассмотрим воздушную линию электропередачи с полным циклом транспозицией фаз. В рамках рассматриваемой задачи фазы воздушной линии расположены в одной плоскости параллельно земле. Данная конструкция линии электропередачи предполагает, что собственные сопротивления и проводимости фаз одинаковые, а взаимные сопротивления и проводимости – различны.
Покажем выравнивание параметров линии электропередачи на базе активно-индуктивной части схемы замещения.
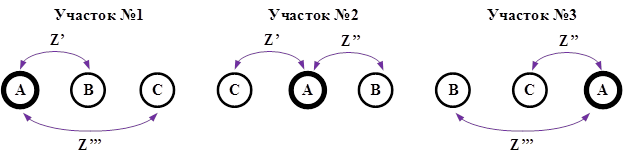
Рис.6. Взаимные индуктивности фазы А при полном цикле транспозиции фаз воздушной линии
Определим падение напряжение фазы А на активно-индуктивном участке схемы замещения:
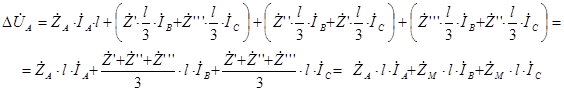
Аналогичный результат можно получить для других фаз активно-индуктивной части схемы замещения, а также для активно-емкостной части схемы замещения.
Таким образом, полный цикл транспозиции на воздушной линии электропередачи усредняет и выравнивает параметры линии: собственные сопротивления фаз, взаимные сопротивления между фазами, собственные проводимости фаз на линии и проводимости между фазами линии.
В результате для транспонированной линии электропередачи можно записать следующие системы уравнений:
1. Для активно-индуктивной части схемы замещения:
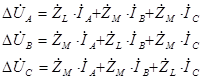
где 
- собственное комплексное сопротивление линии электропередачи, а 
- взаимное комплексное сопротивление линии электропередачи.
2. Для активно-емкостной части схемы замещения
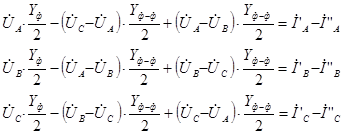
где 
- собственная емкостная проводимость линии электропередачи на землю, а 
- взаимная емкостная проводимость линии электропередачи.
