Трансформатором называют статическое электромагнитное устройство, имеющее две или большее число индуктивно связанных обмоток и предназначенное для преобразования посредством электромагнитной индукции одну систему переменного тока в другую систему переменного тока.
Найдем схемы замещения трехфазного двухобмоточного трансформатора в системе координат прямой, обратной и нулевой последовательности. Система прямой последовательности представляет собой систему из трех векторов ![]() равных по модулю и повернутых друг относительно друга на угол 120 градусов по часовой стрелке. Система обратной последовательности представляет собой систему из трех векторов
равных по модулю и повернутых друг относительно друга на угол 120 градусов по часовой стрелке. Система обратной последовательности представляет собой систему из трех векторов ![]() равных по модулю и повернутых друг относительно друга на угол 120 градусов по часовой стрелке. Система нулевой последовательности представляет собой систему из трех векторов
равных по модулю и повернутых друг относительно друга на угол 120 градусов по часовой стрелке. Система нулевой последовательности представляет собой систему из трех векторов ![]() равных по модулю и совпадающими по фазе.
равных по модулю и совпадающими по фазе.
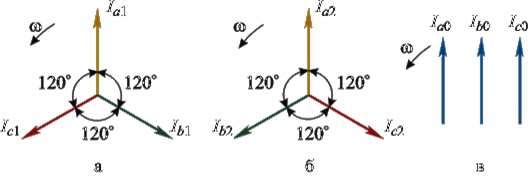
Рис.1. Система координат прямой (а), обратной (б) и нулевой (в) последовательности
Обозначения:
![]() – система токов прямой последовательности;
– система токов прямой последовательности;
![]() – система токов обратной последовательности;
– система токов обратной последовательности;
![]() – система токов нулевой последовательности.
– система токов нулевой последовательности.
Любая несимметричная система ![]() может быть представлена через сумму трех симметричных систем (систему прямой, обратной и нулевой последовательности) следующим образом:
может быть представлена через сумму трех симметричных систем (систему прямой, обратной и нулевой последовательности) следующим образом:
![]()
![]()
![]()
В матричной форме данное уравнение выглядит следующим образом:
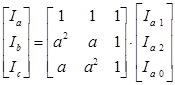
С другой стороны любая симметричная система (система прямой, обратной и нулевой последовательности) может быть представлена через несимметричную систему ![]() следующим образом:
следующим образом:
![]()
![]()
![]()
В матричной форме данное уравнение выглядит следующим образом:
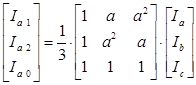
В представленных уравнениях используется оператор поворота «a», который представляет собой вектор единичной длины.
![]()
В случае умножения какого-либо вектора на оператор «a» происходит поворот исходного вектора без изменения его модуля на угол 120 градусов против часовой стрелки. В связи с этим для оператора «a» справедливы следующие соотношения:
![]()
![]()
Все приведенные соотношения справедливы для всех параметров электроэнергетического режима работы: для напряжений, токов и т.п.
Рассмотрим трехфазный двухобмоточный трансформатор со схемой соединения обмоток Y/Δ с 11 группой соединения обмотки. Для простоты дальнейших расчетов будем рассматривать приведенный трансформатор, в котором число витков первичной обмотки приведены к количеству витков вторичной обмотки, а также для простоты письма все используемые комплексные величины в уравнениях будут обозначаться без точек над переменными.
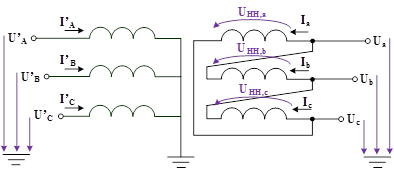
Рис.2. Трехфазный двухобмоточный трансформатор со схемой соединения обмоток Y/Δ
Для обмотки соединённой в треугольник по второму закону Кирхгофа записывается следующая система уравнений для контуров ![]() ,
, ![]() и
и ![]() :
:
![]()
![]()
![]()
Напряжения на первичной обмотке ![]() связаны с напряжениями на вторичной обмотке
связаны с напряжениями на вторичной обмотке ![]() следующей системой уравнений:
следующей системой уравнений:
![]()
![]()
![]()
В результате общая система уравнений, которая описывает связь между напряжениями ![]() и
и ![]() в трансформаторе, перепишется в следующем виде:
в трансформаторе, перепишется в следующем виде:
![]()
![]()
![]()
Перейдем от системы уравнений в фазной системе координат к системе уравнений, записанной для прямой, обратной и нулевой последовательности. Умножим правую и левую части системы уравнений на матрицу преобразований, которая позволяет получить симметричную систему (система прямой, обратной и нулевой последовательности) через параметры фазной системы координат ![]() .
.
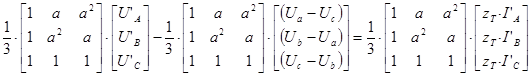
Первое слагаемое рассматриваемой системы перепишется в следующем виде:
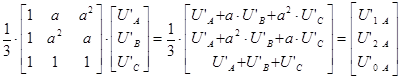
Второе слагаемое рассматриваемой системы перепишется в следующем виде:
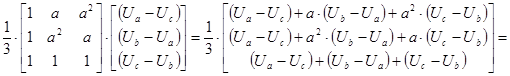
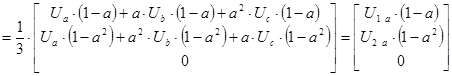
Третье слагаемое рассматриваемой системы перепишется в следующем виде:
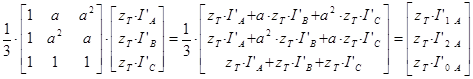
В результате получили систему уравнений, которая описывает процессы происходящие в трехфазном двухобмоточном трансформаторе со схемой соединения обмоток Y/Δ (11 группа) в системе координат прямой, обратной и нулевой последовательности.
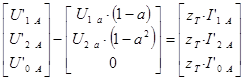
С учетом следующих соотношений (![]() и
и ![]() ) полученная система уравнений может быть переписана в следующем виде:
) полученная система уравнений может быть переписана в следующем виде:
![]()
![]()
![]()
По данной системе уравнений можно составить следующие схемы замещения трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Δ в системе координат прямой, обратной и нулевой последовательности (см. рис.3).
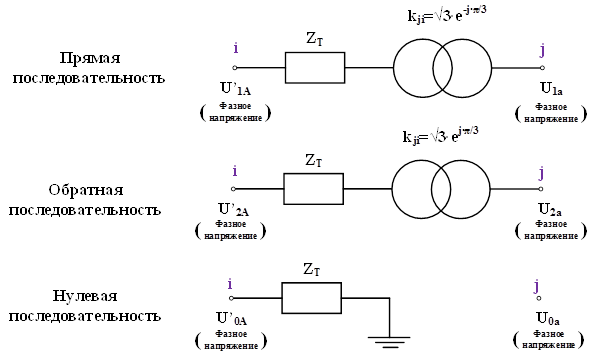
Рис.3. Схемы замещения трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Δ в системе координат прямой, обратной и нулевой последовательности
Схема замещения прямой последовательности трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Δ представляет собой схему содержащую комплексное сопротивление и идеальный трансформатор с коэффициентом трансформации ![]() .
.
Схема замещения обратной последовательности трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Δ представляет собой схему содержащую комплексное сопротивление и идеальный трансформатор с коэффициентом трансформации ![]() .
.
Схема замещения нулевой последовательности трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Δ представляет собой содержащую комплексное сопротивление, которое с одной стороны заземлено (шунт на землю).
Следует заметить, что если обмотка двухобмоточного трансформатора соединённая в звезду имеет изолированную нейтраль, то сопротивление трансформатора для нулевой последовательности представляет собой бесконечно большое сопротивление, т.к. в этом случае вообще исключается циркуляция токов нулевой последовательности в его обмотках.
Рассмотрим трехфазный двухобмоточный трансформатор со схемой соединения обмоток Y/ Y. Для простоты дальнейших расчетов будем рассматривать приведенный трансформатор, в котором число витков первичной обмотки приведены к количеству витков вторичной обмотки, а также для простоты письма все используемые комплексные величины в уравнениях будут обозначаться без точек над переменными.
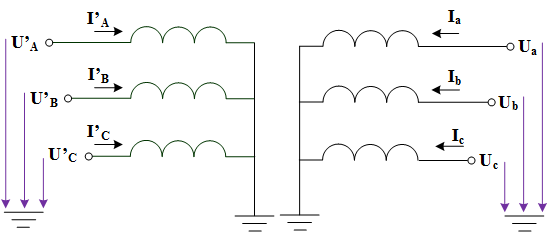
Рис.4. Трехфазный двухобмоточный трансформатор со схемой соединения обмоток Y/ Y
Запишем систему уравнений, которая описывает связь между напряжениями ![]() и
и ![]() в трансформаторе в следующем виде:
в трансформаторе в следующем виде:
![]()
![]()
![]()
Перейдем от системы уравнений в фазной системе координат к системе уравнений, записанной для прямой, обратной и нулевой последовательности. Умножим правую и левую части системы уравнений на матрицу преобразований, которая позволяет получить симметричную систему (система прямой, обратной и нулевой последовательности) через параметры фазной системы координат ![]() .
.
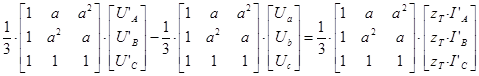
В результате умножения получим систему уравнений, которая описывает процессы происходящие в трехфазном двухобмоточном трансформаторе со схемой соединения обмоток Y/Y в системе координат прямой, обратной и нулевой последовательности.
![]()
![]()
![]()
По данной системе уравнений можно составить следующие схемы замещения трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Y в системе координат прямой, обратной и нулевой последовательности (см. рис.5).
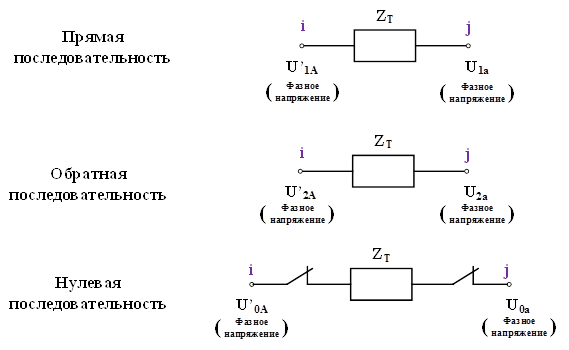
Рис.5. Схемы замещения трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/ Y в системе координат прямой, обратной и нулевой последовательности
Схема замещения прямой, обратной и нулевой последовательности трехфазного двухобмоточного трансформатора со схемой соединения обмоток Y/Y представляет собой схему содержащую комплексное сопротивление.
Следует заметить, что если обмотка двухобмоточного трансформатора, которая соединена в звезду, имеет изолированную нейтраль, то сопротивление трансформатора для нулевой последовательности представляет собой бесконечно большое сопротивление, т.к. в этом случае исключается циркуляция токов нулевой последовательности в его обмотках. Схема замещения нулевой последовательности в таком случае имеет разрыв.