Расчет установившегося режима линейной электрической цепи, которая находится под гармоническим воздействием ЭДС (синусоидальная функция от времени), связан с нахождением частного решения системы неоднородных дифференциальных уравнений. В случае рассмотрения сложной электрической цепи задача определения установившегося режима работы становится труднорешаемой, так как требует трудоёмких и громоздких вычислений.
Для существенного упрощения расчетов установившегося режима работы линейной электрической цепи применяется метод комплексных амплитуд (символический метод или комплексный метод), который основан на идее функционального преобразования, при котором гармоническая функция из временной области (оригинал функции) заменяется функцией, которая определена на комплексной области (изображение исходной функции).
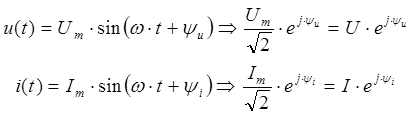
В представленном выражении используются следующие обозначения:
- действующее значение фазного напряжения;
- начальная фаза напряжения;
- действующего значение тока, который протекает в фазе;
- начальная фаза тока.
Следует отметить, что с целью единообразия выполнения расчетов в соответствии с методом комплексных амплитуд было принято на комплексной плоскости изображать векторы синусоидально изменяющихся величин для нулевого момента времени 
.
Комплексное сопротивление определяется отношением напряжения на элементе к току, который протекает в элементе.
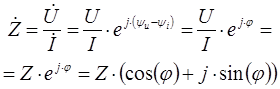
В представленном выражении используются следующие обозначения:
- комплексная величина действующего фазного напряжения;
- комплексная величина действующего тока, который протекает в фазе.
Угол сдвига между током и напряжением 
, который определяется разностью начальной фазы напряжения и начальной фазой тока. Формула для определения угла сдвига между током и напряжением записывается следующим образом:
- Положительный сдвиг фаз между током и напряжением указывает на то, что напряжение по фазе опережает ток. Данный режим работы характеризует активно-индуктивную нагрузку.
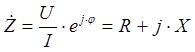
- Отрицательный сдвиг фаз между током и напряжением указывает на то, что напряжение по фазе отстает от тока. Данный режим работы характеризует активно-емкостную нагрузку.
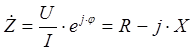
Комплексная мощность определяется произведением комплексного напряжения на сопряженную величину комплексного тока.
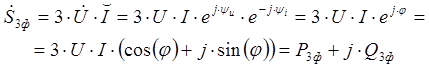
В представленном выражении используются следующие обозначения:
- комплексная величина трехфазной мощности в сети переменного тока;
- трехфазная активная мощность в сети переменного тока;
- трехфазная реактивная мощность в сети переменного тока;
- комплексная величина действующего фазного напряжения;
- сопряженная комплексная величина действующего тока, который протекает в фазе.
Таким образом, вещественная часть комплексной мощности равна активной мощности, а мнимая часть – реактивной мощности. В зависимости от угла сдвига между током и напряжением реактивная мощность принимает разные знаки:
- Положительный сдвиг фаз между током и напряжением обеспечит положительный знак перед реактивной мощностью. Данный режим работы характеризует активно-индуктивную нагрузку.
- Отрицательный сдвиг фаз между током и напряжением обеспечит отрицательный знак перед реактивной мощностью. Данный режим работы будет соответствовать активно-емкостной нагрузке.
Комплексные параметры электроэнергетического режима изображают векторами на комплексной плоскости. Комплексная плоскость с графическим отображением синусоидальных величин при помощи направленных отрезков (векторов) называется векторной диаграммой. Векторные диаграммы позволяют упростить расчет цепей синусоидального тока, так как вместо алгебраического сложения или вычитания мгновенных значений синусоидально изменяющихся величин выполняется сложение или вычитание их векторов. Следует отметить, что анализ векторных диаграмм токов и напряжений является одним из основных способов проверки правильности подключения измерительных цепей ТТ и ТН к устройству релейной защиты и автоматики.
В качестве первого примера рассмотрим векторную диаграмму режимных параметров (токов, напряжений, мощности и сопротивления) для активно-индуктивной нагрузки.
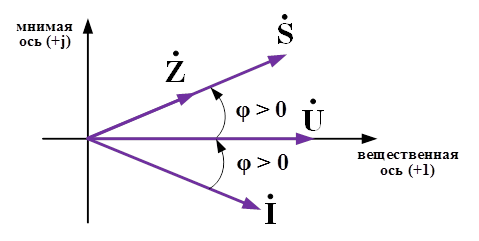
Рис.1. Векторная диаграмма параметров электроэнергетического режима для активно-индуктивной нагрузки
В цепи переменного тока с активно-индуктивной нагрузки вектор тока отстает от вектора напряжения при вращении векторов против часовой стрелки. В таком режиме работы электрической цепи угол сдвига между током и напряжения больше нуля. Вектора полной мощности и полного сопротивления, как видно из векторной диаграммы, будут опережать вектор напряжения на угол сдвига между током и напряжения.
В качестве второго примера рассмотрим векторную диаграмму режимных параметров (токов, напряжений, мощности и сопротивления) для активно-емкостной нагрузки.
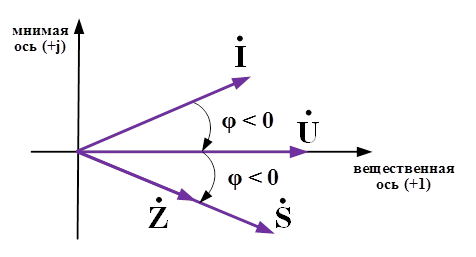
Рис.2. Векторная диаграмма параметров электроэнергетического режима для активно-емкостной нагрузки
В цепи переменного тока с активно-емкостной нагрузки вектор тока опережает вектор напряжения при вращении векторов против часовой стрелки. В таком режиме работы электрической цепи угол сдвига между током и напряжения меньше нуля. Вектора полной мощности и полного сопротивления, как видно из векторной диаграммы, будут отставать от вектора напряжения на угол сдвига между током и напряжения.
