Рассмотрим методику расчета электроэнергетического установившегося режима работы при заданном значении мощности в узлах нагрузки и генерации. Узел нагрузки и узел генерации может моделироваться различными математическими моделями. В случае если нагрузка в узлах расчетной схемы моделируются заданным значением мощности, то система уравнений, которая описывает установившийся режим работы электрической сети, становится нелинейной.
В качестве примера рассмотрим электрическую сеть, которая состоит из трех подстанций, трех линий электропередач, двух узлов с нагрузкой и одним узлом с генерирующим оборудованием. Схема замещения заданной сети представлять собой схему, которая состоит из трех узлов и трех ветвей, при этом каждая линия электропередач представляет собой П-образную схему замещения (обладает продольным сопротивлением и поперечным сопротивлением). Нагрузка и генерация, в данном примере, заменяется нелинейным источником тока, величина которого меняется в зависимости от напряжения в узле и задается в следующем виде:
,
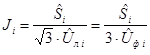- сопряженное значение мощности в узле i, которое определяется следующим выражением: 
;
и 
- сопряженное значение линейного и фазного напряжения в узле i.
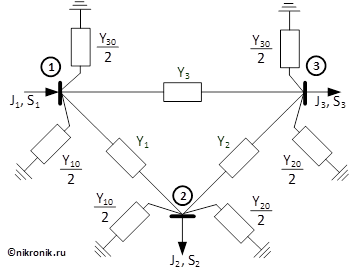
Рис.1. Схема замещения расчетной схемы сети
Для расчета электроэнергетического установившегося режима работы необходимо составить систему уравнений. Формирование системы уравнений будем производить по методу узловых потенциалов (для фазных значений напряжений).
В результате получили систему уравнений, которая состоит из трех уравнений с тремя неизвестными. Записанная система уравнения записана для комплексных переменных: фазные напряжения в узлах расчетной схемы, проводимости и токи в узлах расчетной схемы. В дальнейшем для простоты отображения материала точки над комплексными переменными учитывать не будем.
Описанная система уравнений может моделировать сеть различного класса напряжения. В связи с этим при расчете электрического режима вносят такое понятие, как базисный и балансирующий узел.
Базисным узлом называется узел, в котором задан комплекс напряжения, т.е. модуль напряжения и его угол (или вещественная и мнимая часть комплексного числа). Обычно вектор напряжения в базисном узле ориентируют по вещественной оси комплексной плоскости.
Если в расчетной схеме задан модуль напряжения в одном узле (базисном узле), то число искомых переменных в системе уменьшается на единицу. Для того чтобы привести число уравнений к числу неизвестных необходимо исключить в системе одно из уравнений. Узел, уравнение которого исключается из системы уравнений, называется балансирующим узлом. Задающий ток балансирующего узла определяется после расчета токов во всех ветвях расчетной схемы.
Следует отметить, что «базисный узел» и «балансирующий узел» относится к «особым узлам». К данным узлам также относят так называемый «опорный узел» – генераторный узел с регулируемыми генераторами. Следует отметить, что моделирование узлов генерации PQ- моделями является заведомо неправильным методом. Поведение PQ-модели генератора не соответствует поведению реального генератора при изменении режима сети. Для моделирования генерирующих узлов используют PU- или PEq-модели, которые поддерживают заданные значения модуля напряжения в узлах генерации. Регулируемые генераторы обеспечивают сведение баланса реактивных составляющих токов (мощности) в рассматриваемой схеме.
В качестве базисно-балансирующего узла в расчетной схеме выберем узел «1», тогда система уравнений перепишется в следующем виде (для фазных значений напряжений):
Представленную систему уравнений перепишем в другой форме, выразив ток через сопряженное значение мощности и напряжения в узле. В результате система уравнений перепишется в следующем виде:
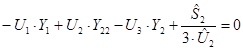
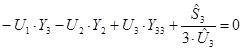
где
; 
.
Следует отметить, что полученная система уравнений записана для фазных значений напряжений в расчетной схеме замещения. В случае использования линейных значений напряжений систему уравнений необходимо умножить на 
.
Умножим систему уравнений, составленных по методу узловых потенциалов, на сопряжённый комплекс напряжения соответствующего узла. В результате получим систему уравнений в форме баланса мощности (для фазных значений напряжений).
Обобщенная формула записи уравнений для k-узла (для фазных значений напряжений):
Рассматриваемая система уравнений является нелинейной, которая записана через комплексные и сопряженные комплексные переменные. Для решения данной нелинейной системы уравнений представленную систему необходимо переписать через равенство вещественных и равенство мнимых переменных уравнения. В результате, представленная система уравнений может быть переписана в следующем виде (система уравнений с вещественными переменными и системы уравнений с мнимыми переменными):
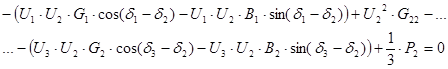
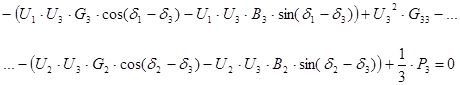
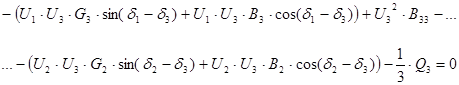
Данная система уравнений была записана с учетом следующих соотношений:
Полученная система уравнений является нелинейной. Решение нелинейной системы уравнений будем проводить по методу Ньютона, который является основным методом для решения системы уравнений, которая описывает установившийся режим работы электрической сети. Идея метода Ньютона состоит в последовательной замене на каждой итерации системы нелинейных уравнений некоторой линейной системой, решение которой дает значения неизвестных, более близкие к решению нелинейной системы, чем исходное приближение.
где
- вектор столбец неизвестных параметров (напряжений и углов) на текущем шаге итерации;
- вектор столбец неизвестных параметров (напряжений и углов) на предыдущем шаге итерации;
- вектор столбец значений функций балансов мощности в узлах при заданных значениях напряжения на предыдущем шаге итерации;
- матрица Якоби (якобиан системы нелинейных уравнений), которая представляет собой матрицу значений частных производных функций балансов мощности в узлах при заданных значениях напряжения на предыдущем шаге итерации.
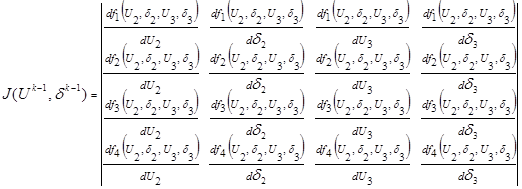
Функции балансов мощности в узлах определяются из системы нелинейных уравнений следующим образом:
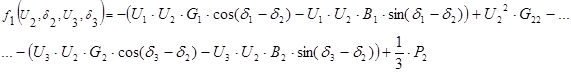
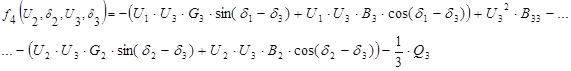
Обобщенная формула записи уравнений для описания балансов активной и реактивной мощности для k-узла (для фазных значений напряжений):
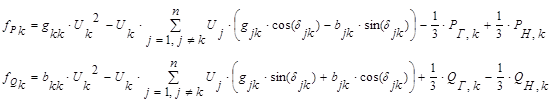
где взаимный угол 
отсчитывается от вектора напряжений k-го узла к вектору напряжения j-го узла против часовой стрелки
На каждом шаге итерационного процесса вычисляется вектор столбец напряжений и абсолютных углов 
. Итерационный процесс продолжается до тех пор, пока не будет достигнута заданная точность расчета установившегося режима работы:
где 
- заданная погрешность расчета, которая отражает точность определения напряжений в узлах расчетной схемы.
После определения значений напряжений в узлах расчетной схемы определяют значения токов в ветвях расчетной схемы, используя второй закон Кирхгофа. Прежде чем записать уравнения необходимо в схеме замещения обозначить направление токов и напряжений в расчетной схеме. Направление токов и напряжений расставим в соответствии с приведённой схемой (см. рис.2)
Рис.2. Ветви расчетной схемы
Значение тока в рассматриваемой ветви будет определяться в соответствии со следующим выражением:
где
и 
- комплексные значения фазного напряжения в начале и в конце рассматриваемой линии.
Значение перетока полной мощности в ветви будет определяться в соответствии со следующими выражениями:
- мощность в начале ветви: 
;
- мощность в конце ветви: 
.
В записанных выше формулах использовались следующие обозначения:
- и - комплексные значения фазного напряжения в начале и в конце рассматриваемой линии;
- 
- сопряженное значение тока в ветви.
В результате выполнения расчета установившегося режима электрической сети определяются значения векторов напряжения в узлах расчетной схемы, значения токов и перетоков активной и реактивной мощности в ветвях расчетной схемы.
