Электрическая цепь представляет собой совокупность электрических элементов (резисторов, катушек индуктивностей, батарей конденсаторов, постоянные и переменные источники напряжения и т.д.), которые соединены между собой таким образом, что в полученном замкнутом контуре протекает электрический ток.
Для определения действующих (или мгновенных) значений токов и падений напряжений на элементах электрической цепи необходимо выполнить следующую последовательность действий:
- Этап 1.Составитьсхему замещения электрической цепи, в которой реальные элементы заменяются идеализированными элементами электрической цепи (активное сопротивление, индуктивность, емкость, ЭДС и т.д.).
- Этап 2.Обозначить на схеме замещения условно положительное направление токов в ветвях и падение напряжения на элементах расчетной схемы замещения. Следует отметить, что в качестве положительного направления падения напряжения выбирают направление, которое совпадает с направлением тока в ветви расчетной схемы замещения.
- Этап 3.Записать систему уравнений, которая связывает напряжения и токи, по одному из следующих способов:
– 1-ого и 2-ого закона Кирхгофа;
– метод контурных токов;
– метод узловых потенциалов.
Каждый из представленных методов позволяет получить необходимый результат, но при разном количестве записанных уравнений в исходной системе уравнений. Следует отметить, что данные методы справедливы как для мгновенных значений токов и напряжений, так и для векторных переменных токов и напряжений.
- Этап 4.Выполнить расчет записанной системы уравнений и определить величины напряжения, токов,перетоков активной и реактивной мощности в ветвях расчетной схемы.
Составление системы уравнений, используя первый и второй закон Кирхгофа.
Первый и второй законы Кирхгофа обеспечивают связь между токами и напряжениями на участках любой электрической цепи. Впервые законы были сформулированы Густавом Кирхгофом в 1845 году. Данные законы вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле).
Первый закон Кирхгофа - алгебраическая сумма токов в каждом узле расчетной схемы равна нулю. Данное утверждение справедливо как для мгновенных значений, так и для векторных значений.
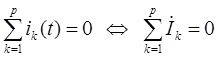
где p – количество ветвей, которые присоединены к рассматриваемому узлу расчетной схемы.
При составлении уравнений согласно первому закону Кирхгофа со знаком «плюс» записываются токи, направленные к узлу, а со знаком «минус» записываются токи, направленные от узла.
Формулировка данного закона может быть переписана в следующем виде: алгебраическая сумма токов, втекающих в узел расчетной схемы, равна алгебраической сумме токов, вытекающих из узла расчетной схемы.
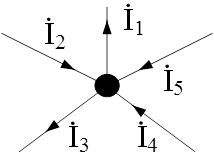
Рис.1. Пояснение к первому закону Кирхгофа
Второй закон Кирхгофа - алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС действующих в этом контуре. Данное утверждение справедливо как для мгновенных значений, так и для векторных значений.
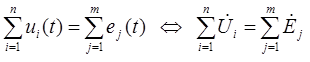
где n – число ветвей в замкнутом контуре;
m – число источников ЭДС.
При составлении уравнений согласно второму закону Кирхгофа со знаком «плюс» записываются падения напряжения (или ЭДС) направление которых совпадает с направлением обхода контура, а со знаком «минус» записываются падения напряжения (или ЭДС) направление которых противоположно направлению обхода контура
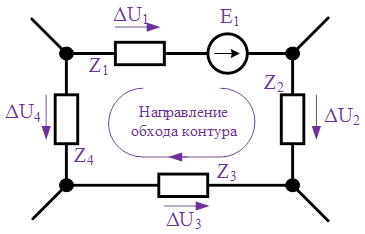
Рис.2. Пояснение ко второму закону Кирхгофа
В качестве примера рассмотрим расчетную схему замещению, которая состоит из двух источников ЭДС и трех сопротивлений. Произвольно выберем положительные направления токов и падений напряжений во всех ветвях расчётной схемы, а также выберем направление обхода во всех контурах.
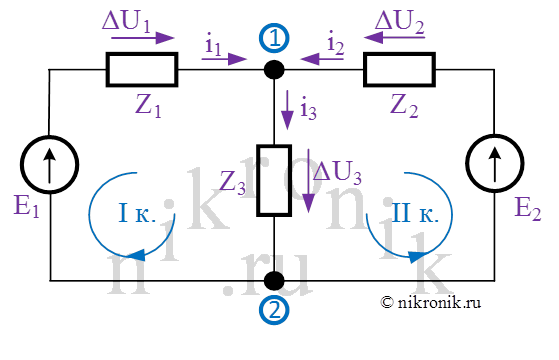
Рис.3. Расчетная схема замещения для пояснения первого и второго закона Кирхгофа.
Рассматриваемая схема замещения состоит из 2 узлов (q = 2) и 3 ветвей (p = 3). В соответствии с первым законом Кирхгофа можно записать одно уравнение (q – 1):
В соответствии со вторым законом Кирхгофа можно записать два уравнения (p – q + 1):
В результате была получена система уравнений, которая позволяет определить токи во всех ветвях расчетной схемы исходя из заданных значений ЭДС и сопротивлений.
Составление системы уравнений, используя метод контурных токов
Метод контурных токов позволяет упростить расчет электрических цепей по сравнению с методом по первому и второму законам Кирхгофа за счет уменьшения числа уравнений. Данный метод основан на применении второго закона Кирхгофа.
При выполнении расчета методом контурных токов необходимо выбрать одинаковое направление обхода в каждом рассматриваемом контуре (либо по часовой стрелке, либо против часовой стрелке). Далее в соответствии с данным методом записывается система уравнений относительно контурных токов, которые протекают в каждом независимом контуре, используя следующие правила:
Правило №1. В левой части i-го уравнения записываются:
- со знаком «+» записывается произведение контурного тока i-го контура на сумму сопротивлений всех звеньев, входящих в контур;
- со знаком «-» записывается остальные контурные токи, умноженные на суммы сопротивлений звеньев, по которым i-ый контур пересекается с этими контурами.
- ток i-го контура, для которого записывается уравнение;
- сопротивления звеньев, входящих в i-ый контур;
- токи соседних контуров, который пересекаются с i-ым контуром;
- сопротивления звеньев, по которым i-ый контур пересекается с другими контурами.
Правило №2. В правой части i-го уравнения записывается сумма источников ЭДС с учётом знаков («плюс» — если направления ЭДС и обхода контура совпадают, в противном случае – «минус»), а также добавляются источники тока, умноженные на сопротивление соответствующего звена с учётом знаков («плюс» — если направления источника тока и обхода контура совпадают, в противном случае – «минус»)
- источники ЭДС, которые входят в i-ый контур;
- произведение тока и сопротивление ветви с источником тока, которые входят в i-ый контур.
Заключительным этапом определяются токи во всех ветвях расчетной схемы по найденным значениям контурных токов.
В качестве примера рассмотрим расчетную схему замещению, которая состоит из двух источников ЭДС и трех сопротивлений. Произвольно выберем положительные направления обхода в каждом рассматриваемом контуре: направление по часовой стрелке.
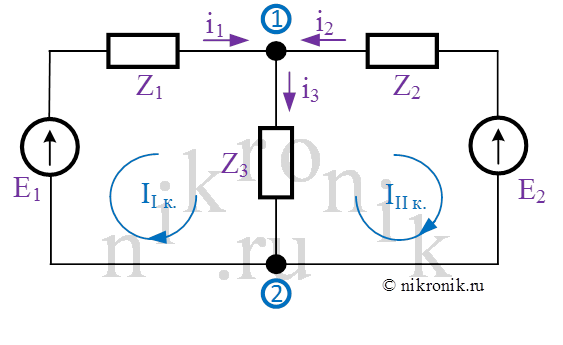
Рис.4. Расчетная схема замещения для пояснения метода контурных токов.
Рассматриваемая схема замещения состоит из 2 узлов (q = 2) и 3 ветвей (p = 3), таким образом, в расчетной схеме замещения можно выделить два независимых контура. В соответствии с методом контурных токов можно записать два уравнения (p – q + 1):
В результате была получена система уравнений, которая позволяет определить контурные токи исходя из заданных значений ЭДС и сопротивлений. Заключительным этапом расчета будет являться процесс определения токов во всех ветвях расчетной схемы по найденным значениям контурных токов.
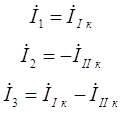
Составление системы уравнений, используя метод узловых потенциалов
Метод узловых потенциалов позволяет упростить расчет электрических цепей по сравнению с методом по первому и второму законам Кирхгофа за счет уменьшения числа уравнений. Данный метод основан на применении первого закона Кирхгофа.
При выполнении расчета методом узловых потенциалов необходимо выбрать один узел, в котором потенциал узла приравнивается к нулю. Остальные потенциалы узлов расчетной схемы определяются относительно узла с нулевым потенциалом. Далее в соответствии с данным методом записывается система уравнений, относительно потенциалов узлов расчетной схемы, используя следующие правила:
Правило №1. В левой части i-го уравнения записываются:
- со знаком «+» потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу;
- со знаком «-» потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
- потенциал i-го узла, для которого записывается уравнение;
- сумму проводимостей ветвей, присоединенных к данному i-му узлу;
- потенциал k-го узла, который связан через ветвь с i-ым узлом;
- проводимость ветви, которая связывает i-ый и k-ый узел.
Правило №2. В правой части i-го уравнения записывается так называемый узловой ток, который равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “–”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
- источники тока, которые присоединены к i-му узлу;
- произведение ЭДС и проводимости ветви с источником ЭДС, которые присоединены к i-му узлу.
В качестве примера рассмотрим расчетную схему замещению, которая состоит из двух источников ЭДС и трех сопротивлений. В одном из рассматриваемых узлов расчетной схеме обозначим нулевой потенциал.
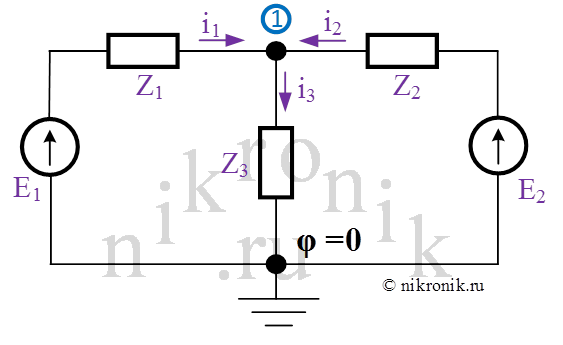
Рис.5. Расчетная схема замещения для пояснения метода узловых потенциалов.
В соответствии с методом узловых потенциалов можно записать одно уравнение (q - 1):
В результате была получена система уравнений, которая позволяет определить потенциал узлов рассматриваемой схемы замещения исходя из заданных значений ЭДС и сопротивлений. Заключительным этапом расчета будет являться процесс определения токов во всех ветвях расчетной схемы по найденным значениям потенциалов узлов рассматриваемой схемы замещения.
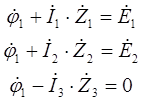
Представленные выше методы позволяют определять токи и напряжения в ветвях расчетной схемы для любой электрической цепи постоянного и переменного тока.
