Любую систему автоматического регулирования (САР) можно представить в виде структурной схемы, в которой отдельные элементы системы изображаются в виде звеньев, соединенных определенным образом между собой. Для нахождения передаточной функции системы автоматического регулирования необходимо выполнить эквивалентирование ее структурной схемы на основе замены групп звеньев эквивалентными передаточными функциями с помощью правил переноса воздействий.
При составлении структурных схем систем автоматического регулирования кроме условного изображения звена (рисунок 1) используются следующие символы, смысл которых ясен из приведенных ниже схем.
- знак разветвления сигнала
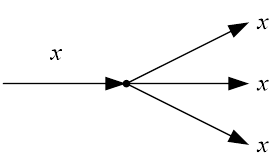
- знак алгебраического суммирования сигналов
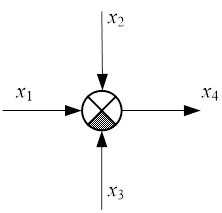
или
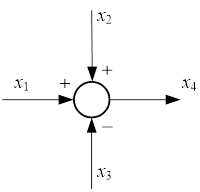
х4 = х1 + х2 - х3.
П.1. Последовательное соединение звеньев
Последовательным называется такое соединение звеньев, при котором выходная величина одного звена подается на вход последующего звена

Рисунок 1. Последовательное соединение звеньев
Совокупность последовательно соединенных n однородных звеньев можно заменить одним звеном, передаточная функция которого равна произведению передаточных функций исходных звеньев.
![]()
Другими словами, эквивалентная передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев.
П.2. Параллельное соединение звеньев
Параллельным называется такое соединение звеньев, при котором на вход всех звеньев подается один и тот же сигнал, а выходные сигналы от всех звеньев суммируются.
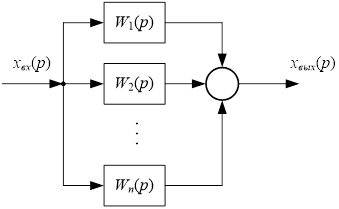
Рисунок 2. Параллельное соединение звеньев
Совокупность параллельно соединенных однородных звеньев можно заменить одним звеном, передаточная функция которого есть сумма передаточных функций звеньев.
![]()
Параллельным соединением в данном случае принимается такое соединение звеньев, когда на вход всех звеньев подается одна и та же величина, а выходная величина формируется как сумма выходных величин всех звеньев.
П.3. Соединение с обратной связью (звено, охваченное обратной связью)
Обратной связью называется цепь передачи воздействий с выхода звена (системы) на ее вход. Обратная связь образует путь передачи воздействия в дополнение к основной цепи воздействия. Обратная связь позволяет контролировать и учитывать действительное состояние управляемой системы (т. е., в конечном счёте, результаты работы управляющей системы) и вносить соответствующие корректировки в её алгоритм управления.
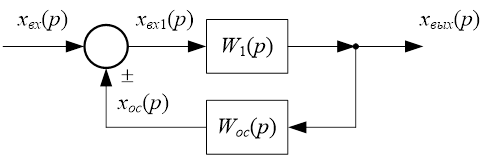
Рисунок 3. Структурная схема с обратной связью
Обратные связи бывают отрицательные и положительные. При отрицательной обратной связи воздействие ![]() , поступающее на вход звена в прямой цепи, равно разности воздействий
, поступающее на вход звена в прямой цепи, равно разности воздействий ![]() и
и ![]() , а при положительной — их сумме.
, а при положительной — их сумме.
![]()
В данном выражении переменная ![]() определяется через передаточную функцию
определяется через передаточную функцию ![]() следующим образом:
следующим образом:
![]()
В представленном выражении знак "+" соответствует положительной обратной связи, а знак "-" соответствует отрицательной обратной связи.
Для того, чтобы найти эквивалентную передаточную функцию звена, охваченного обратной связью запишем выражение, которое связывает выходную величину ![]() и входную величину
и входную величину ![]() .
.
![]()
Из полученного выражения выразим искомую передаточную функцию
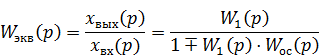
Важно обратить внимание, что при получении последнего выражения знаки, соответствующие положительной и отрицательной обратной связи поменялись на противоположные. Поэтому, в последнем выражении знак "-" соответствует положительной обратной связи, а знак "+" – отрицательной.
П.4. Правила переноса воздействий
При структурных преобразованиях бывает необходимо поменять местами узлы суммирования или точки ветвления, либо перенести какую-то из этих точек через звено. Перенос возмущения в другую точку структурной схемы не должен отразиться на эффекте его действия на системе автоматического регулирования в целом. Поэтому перенос возмущений связан с включением в их цепь согласующих звеньев, передаточные функции которых выбираются из условия, чтобы действие возмущения на систему осталось неизменным.
Перенос воздействий позволяет отдельные фрагменты структурной схемы свести к рассмотренным выше трем видам соединения звеньев.
Правила переноса воздействий, при которых сохраняется эквивалентность структурных схем, достаточно просты и иллюстрируются ниже.
П.4.1. Перенос точки суммирования
Методика переноса точки суммирования заключается в том, что должна сохраняться прежней связь между входной величиной ![]() и величиной в точке разветвления.
и величиной в точке разветвления.
Покажем способ переноса воздействия ![]() на выход или на вход расчетной схемы.
на выход или на вход расчетной схемы.
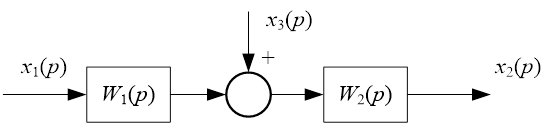
Рис.4 Исходная схема
![]() .
.
П.4.1.1. Перенос на выход
Рассмотрим случай, когда требуется перенести воздействие ![]() по направлению передачи главного воздействия (в конец структурной схемы).
по направлению передачи главного воздействия (в конец структурной схемы).
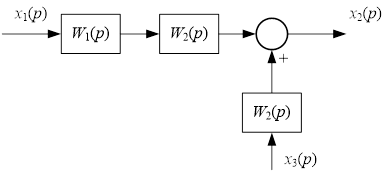
Таким образом, внешнее воздействие ![]() , приложенное в схеме, можно перенести на его вsход, добавив между воздействием и входом звена звено с передаточной функцией
, приложенное в схеме, можно перенести на его вsход, добавив между воздействием и входом звена звено с передаточной функцией
![]()
П.4.1.2. Перенос на вход
Рассмотрим случай, когда требуется перенести воздействие ![]() против направления передачи главного воздействия (в начало структурной схемы).
против направления передачи главного воздействия (в начало структурной схемы).
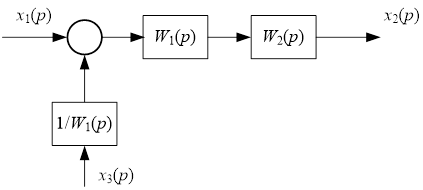
Таким образом, внешнее воздействие ![]() , приложенное в схеме, можно перенести на его вход, добавив между воздействием и входом звена звено с передаточной функцией
, приложенное в схеме, можно перенести на его вход, добавив между воздействием и входом звена звено с передаточной функцией
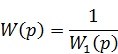
Перенос воздействия в конец или в начало структурной схемы не меняет общей передаточной функции между входной величиной ![]() и выходной величиной
и выходной величиной ![]() .
.
П.4.2. Перенос точки разветвления
Методика переноса точки разветвления заключается в том, что должна сохраняться прежней связь между входной величиной ![]() и величиной в точке разветвления.
и величиной в точке разветвления.
Покажем способ переноса воздействия ![]() на выход или на вход расчетной схемы.
на выход или на вход расчетной схемы.
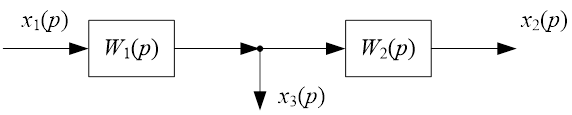
![]() .
.
П.4.2.1. Перенос на выход
Рассмотрим случай, когда требуется перенести воздействие ![]() по направлению передачи главного воздействия (в конец структурной схемы).
по направлению передачи главного воздействия (в конец структурной схемы).
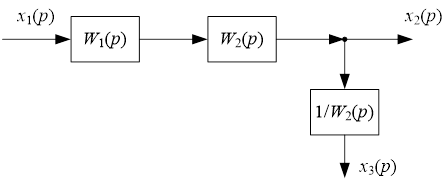
Таким образом, внешнее воздействие ![]() , приложенное в схеме, можно перенести на его вsход, добавив между воздействием и входом звена звено с передаточной функцией
, приложенное в схеме, можно перенести на его вsход, добавив между воздействием и входом звена звено с передаточной функцией
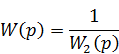
П.4.2.2. Перенос на вход
Рассмотрим случай, когда требуется перенести воздействие ![]() против направления передачи главного воздействия (в начало структурной схемы).
против направления передачи главного воздействия (в начало структурной схемы).
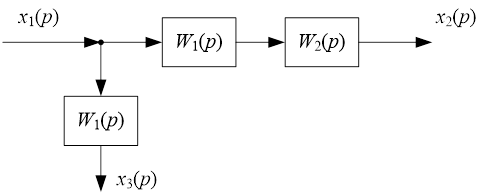
Таким образом, внешнее воздействие ![]() , приложенное в схеме, можно перенести на его вход, добавив между воздействием и входом звена звено с передаточной функцией
, приложенное в схеме, можно перенести на его вход, добавив между воздействием и входом звена звено с передаточной функцией
![]()
Перенос воздействия в конец или в начало структурной схемы не меняет общей передаточной функции между входной величиной ![]() и выходной величиной
и выходной величиной ![]() .
.
Используя полученные выражения передаточных функций типовых соединений звеньев, можно сложную структурную схему системы привести к схеме, состоящей из ряда последовательно включенных звеньев и тем самым облегчить определение передаточной функции системы.