Рассмотрим линейную электрическую цепь с сосредоточенными параметрами, находящуюся под гармоническим воздействием ЭДС (синусоидальная функция от времени). Определение значений токов и напряжений в рассматриваемой схеме сводится к составлению и решению системы дифференциальных уравнений с постоянными коэффициентами, которые могут быть записаны в следующем виде:
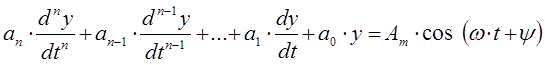
В общем виде решение данного дифференциального уравнения будет определяться суммой двух составляющих: свободной и вынужденной составляющей.
Свободная составляющая представляет собой общее решение системы однородных линейных дифференциальных уравнений, составленных для схемы цепи после коммутации. Свободная составляющая определяет процессы, которые возникают в электрической цепи, выведенной из состояния покоя некоторым воздействием. Свободная составляющая характеризует процесс обмена энергией между индуктивными и емкостными элементами электрической цепи, частота колебаний свободной составляющей определяется параметрами расчетной цепи. В линейных электрических цепях свободные составляющие затухают во времени по экспоненциальному закону.
Вынужденная составляющая представляет собой частное решение системы однородных линейных дифференциальных уравнений, составленных для схемы цепи после коммутации. Вынужденная составляющая определяет установившийся режим работы системы после окончания переходного процесса. Данная составляющая может также называться установившейся составляющей.
В большинстве решаемых задач рассматривают только квазистационарные режимы работы энергосистемы (установившийся режим работы), в связи с этим рассматривают только вынужденную составляющую, а свободной составляющей пренебрегают. В таком случае для расчёта сложной электрической цепи с гармоническими источниками ЭДС широко применяется метод комплексных амплитуд. Данный метод в технической литературе может встречаться под другими названиями: символический метод или комплексный метод, так как он основан на символическом изображении действительных синусоидальных функций времени комплексными числами. Данный метод разработан в конце XIX века американскими инженерами - электротехниками Ч.П.Штейнметцем и А.Е.Кеннели.
Метод комплексных амплитуд, основан на идее функционального преобразования, при котором гармоническая функция из временной области (оригинал функции) заменяется функцией, которая определена на комплексной области (изображение исходной функции). Переход от реальных гармонических токов и напряжений к комплексным амплитудам осуществляется с помощью формулы Эйлера, которая связывает комплексную экспоненту с тригонометрическими функциями.
Формула Эйлера позволяет определить тригонометрические функции через комплексные величины, которые записываются через экспоненты с мнимыми аргументами:
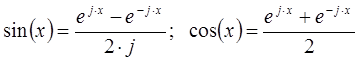
- Рассмотрим случай, когда гармонический сигнал представлен в виде косинусоидальной функции. В рассматриваемом случае в соответствиис представленными выражениями гармоническая функция, заданная во временной области, переписывается в виде двух экспонент в следующем виде:
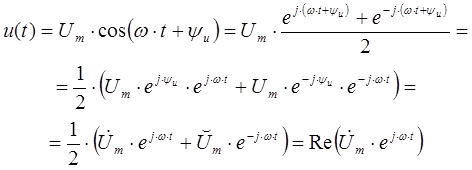
Таким образом, оригинал косинусоидальной функции определяется проекцией комплексного числа на вещественную ось. В представленном выражении используются следующие обозначения:
- комплексная амплитуда, которая определяется по формуле: 
- сопряженная комплексная амплитуда, которая определяется по формуле: 
- оператор вращения, который имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью 
. Всякий неподвижный вектор, будучи умноженным на оператор вращения, начинает вращаться в комплексной плоскости против часовой стрелки с заданной угловой скоростью.
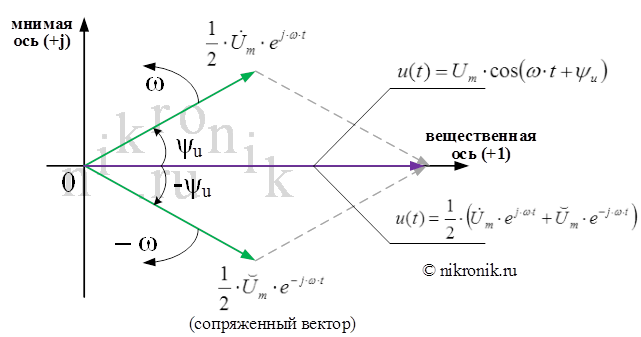
Рис.1. Разложение косинусоидальной функции в виде двух векторов
Таким образом, символическое изображение косинусоидальной функции (оригинала функции) определяется при заданной частоте ω вектором, который характеризуется двумя величинами - амплитудой и начальной фазой.
- Рассмотрим другой случай, когда гармонический сигнал представлен в виде синусоидальной функции. В рассматриваемом случае в соответствиис представленными выражениями гармоническая функция, заданная во временной области, переписывается в виде двух экспонент в следующем виде:
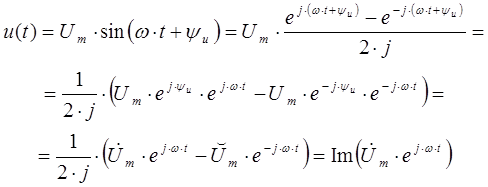
Таким образом, оригинал синусоидальной функции определяется проекцией комплексного числа на мнимую ось. В представленном выражении используются следующие обозначения:
- комплексная амплитуда, которая определяется по формуле:
- сопряженная комплексная амплитуда, которая определяется по формуле:
- оператор вращения, который имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью . Всякий неподвижный вектор, будучи умноженным на оператор вращения, начинает вращаться в комплексной плоскости против часовой стрелки с заданной угловой скоростью.
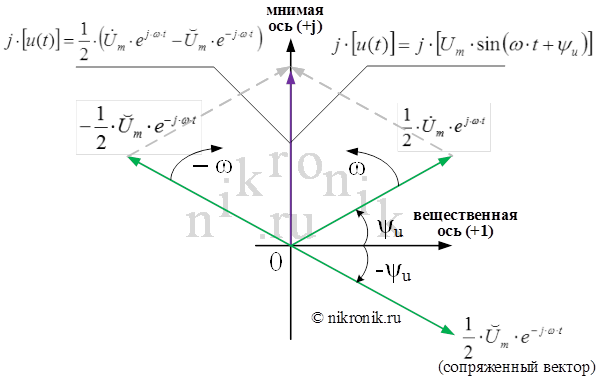
Рис.2.Разложение синусоидальной функции в виде двух векторов
Таким образом, символическое изображение синусоидальной функции (оригинала функции) определяется при заданной частоте ω вектором, который характеризуется двумя величинами - амплитудой и начальной фазой.
Использование метода комплексных амплитуд значительно упрощает расчет линейной электрической цепи, так как операции дифференцирования и интегрирования сводятся к задаче решения системы алгебраических уравнений: операция дифференцирование гармонической функции соответствует умножение комплексного числа на переменную «jω»,а операция интегрирование гармонической функции соответствует делению комплексного числа на «jω».
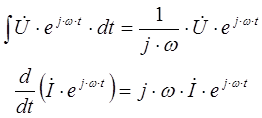
Объединяя полученные результаты можно сделать вывод, что любую гармоническую функцию с заданной частой ω можно представить в виде вектора на комплексной плоскости, который вращается с угловой скоростью ω. С целью единообразия выполнения расчетов в соответствии с методом комплексных амплитуд было принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для нулевого момента времени 
. Таким образом, символическое изображение синусоидальной функции определяется в следующем виде:
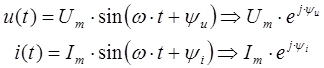
Для определения интенсивности действия электрических параметров (тока или напряжения) используют действующие комплексные значения, которые определяются следующим образом:
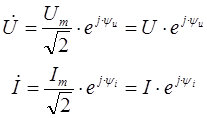
Расчет цепи синусоидального тока методом комплексных амплитуд проводится в следующем порядке:
- На первом этапе гармоническая функция, заданная во временной области, заменяется изображением данной функции на комплексной плоскости.
- На втором этапе составляется система уравнений, которая описывает рассматриваемую электрическую цепь, в соответствии с любым методом расчета электрических цепей. Далее выполняется расчет данной системы уравнений с определением комплексных значений искомых токов и напряжений.
- На третьем этапе выполняют обратное преобразование, с помощью которого переходят от изображения функции на комплексной плоскости к оригиналам функции во временной области. Чтобы восстановить исходное гармоническое колебание по известной комплексной амплитуде и частоте ω, необходимо комплексную амплитуду умножить на 
, а затем выделить мнимую часть (для синусоидальной функции).
Комплексное сопротивление электрической цепи
Определим комплексное сопротивление пассивных элементов электрической цепи, которые находятся под гармоническим воздействием. Для этого рассмотрим связь между током и напряжением на активном, индуктивном и емкостном элементах.
- Рассмотрим активное сопротивление, по которому протекает синусоидальный ток. Данный ток создает в активном напряжении падение напряжение на элементе, которое определяется в следующем виде:
Перепишем данную формулу для изображений синусоидальных функции в следующем виде:
Для нулевого момента времени данное выражение записывается в следующем виде:
Из полученного выражения видно, что ток на индуктивности совпадает по фазе с напряжением. Сопротивление на индуктивности носит активный характер и определяется в следующем виде: 
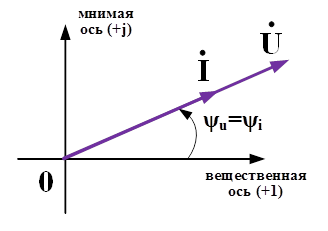
Рис.3. Векторная диаграмма токов и напряжений на резистивном элементе
- Рассмотрим индуктивный элемент, по которому протекает синусоидальный ток. Данный ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции. Таким образом, падение напряжение на элементе определяется в следующем виде:
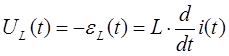
Перепишем данную формулу для изображений синусоидальных функции в следующем виде:
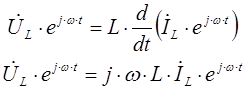
Для нулевого момента времени данное выражение записывается в следующем виде:
Из полученного выражения видно, что ток на индуктивности отстает от напряжения на угол 90 градусов. Сопротивление на индуктивности носит реактивный характер и определяется в следующем виде: 
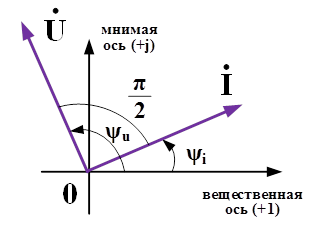
Рис.4. Векторная диаграмма токов и напряжений на индуктивном элементе
- Рассмотрим емкостной элемент, к которому приложено синусоидальное напряжение. Под действием синусоидального напряжения конденсатор будет периодически заряжаться и разряжаться. Периодическая перезарядка конденсатора будет сопровождаться протеканием тока. Таким образом, ток, протекающий между обкладками конденсатора, будет определяться следующим образом:
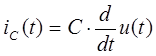
Перепишем данную формулу для изображений синусоидальных функции в следующем виде:
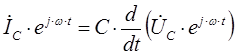
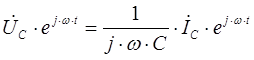
Для нулевого момента времени данное выражение записывается в следующем виде:
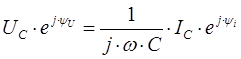
Из полученного выражения видно, что ток на емкости опережает напряжение на угол 90 градусов. Сопротивление на емкости носит реактивный характер и определяется в следующем виде: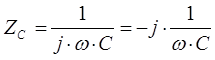 
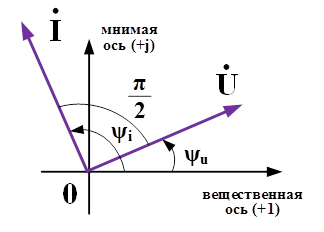
Рис.5. Векторная диаграмма токов и напряжений на емкостном элементе
Следует отметить, что для определения изображений синусоидальных функции (токов и напряжений) в электрической цепи необходимо составить систему уравнений любым доступным методом:
- с помощью первого и второго закона Кирхгофа, который записывается для изображений синусоидальных функции;
- с помощью метода контурных токов, который записывается для изображений синусоидальных функции;
- с помощью метода узловых потенциалов, который записывается для изображений синусоидальных функции.
