Установившийся режим работы электроэнергетической системы рассчитывают при различных способах задания исходных данных в зависимости от физической сути и цели расчета. Рассмотрим наиболее простой случай расчета электроэнергетического режима, когда нагрузка и генерация задается постоянной величиной током. Следует отметить, что в случае если нагрузка в узлах расчетной схемы задается постоянной величиной током, то система уравнений, которая описывает установившийся режим работы электрической сети, является линейной.
В качестве примера рассмотрим электрическую сеть, которая состоит из трех подстанций, трех линий электропередач, двух узлов с нагрузкой и одним узлом с генерирующим оборудованием. Схема замещения заданной сети представлять собой схему, которая состоит из трех узлов и трех ветвей, при этом каждая линия электропередач представляет собой П-образную схему замещения (обладает продольным сопротивлением и поперечным сопротивлением). Нагрузка и генерация, в данном примере, заменяется источником тока с постоянным значением.
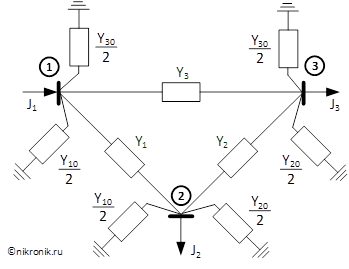
Рис.1. Схема замещения расчетной схемы сети
Расчет установившегося режима выполняется для определения модулей напряжения в узлах расчетной схемы, величины токов, а также перетоков активной и реактивной мощности в ветвях расчетной схемы, определение потерь активной и реактивной мощности в элементах сети. Математически данная задача формулируется как решение системы уравнений, которая описывает баланс токов и напряжений в расчетной схеме. Система уравнений может составляться на основании следующих методов:
– 1-ого и 2-ого закона Кирхгофа;
– метода контурных токов;
– метода узловых потенциалов.
Каждый из представленных методов дает правильный результат, но при разном количестве записанных уравнений в исходной системе уравнений. При расчете установившегося режима в электроэнергетической системе в большинстве случаев пользуются методом узловых потенциалов, так как при решении данным методом необходимо записывать наименьшее количество уравнений в системе уравнений.
В качестве примера, приведем количество уравнений, которое необходимо записать для расчетной схемы (см. рис. 1), в зависимости от используемого метода расчета:
- в соответствии с 1-ым и 2-ым законами Кирхгофа для схемы замещения необходимо записать систему из 6 уравнений;
- в соответствии с методом контурных токов для схемы замещения необходимо записать систему из 4 уравнений;
- в соответствии с методом узловых потенциалов для схемы замещения необходимо записать систему из 3 уравнений.
Как видно из представленного примера для схем замещения электроэнергетической системы в соответствии с методом узловых потенциалов записывается наименьшее количество уравнений. Система уравнений по методу узловых потенциалов могут быть составлены формальным путем с помощью следующих правил:
Правило №1. В левой части i-го уравнения записывается со знаком “+” потенциал i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i-му узлу, и со знаком “–” потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i-му и k-му узлам.
Правило №2. В правой части i-го уравнения записывается так называемый узловой ток, который равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “–”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.
Также следует отметить, что метод узловых потенциалов позволяет составить систему уравнений относительно потенциалов узлов. Однако при расчете электрического режима потенциалы в узлах равны фазному напряжению данных узлов при условии, что точка нулевого потенциала – является землей.
В соответствии с записанными правилами составим полную систему уравнений по методу узловых потенциалов для расчета электроэнергетического установившегося режима:
В результате получили систему уравнений, которая состоит из трех уравнений с тремя неизвестными. Записанная система уравнения записана для комплексных переменных: фазные напряжения в узлах расчетной схемы, проводимости и токи в узлах расчетной схемы. В дальнейшем для простоты отображения материала точки над комплексными переменными учитывать не будем.
Описанная система уравнений может моделировать сеть различного класса напряжения. В связи с этим при расчете электрического режима вносят такое понятие, как базисный и балансирующий узел.
Базисным узлом называется узел, в котором задан комплекс напряжения, т.е. модуль напряжения и его угол (или вещественная и мнимая часть комплексного числа). Обычно вектор напряжения в базисном узле ориентируют по вещественной оси комплексной плоскости.
Если в расчетной схеме задан модуль напряжения в одном узле (базисном узле), то число искомых переменных в системе уменьшается на единицу. Для того чтобы привести число уравнений к числу неизвестных необходимо исключить в системе одно из уравнений. Узел, уравнение которого исключается из системы уравнений, называется балансирующим узлом. Задающий ток балансирующего узла определяется после расчета токов во всех ветвях расчетной схемы.
В качестве базисно-балансирующего узла в расчетной схеме выберем узел «1», тогда система уравнений перепишется в следующем виде:
В результате получена система уравнений, которая имеет два уравнения и в состав уравнений входят две неизвестные величины (напряжение U2 и U3). В связи с тем, что по условиям задачи нагрузка и генерация в узлах представлена током, то данная система представляет собой систему линейных алгебраических уравнений (далее - СЛАУ), которая решается известными способами. Представленная система СЛАУ имеет однозначное и единственное решение.
После определения значений напряжений в узлах расчетной схемы определяют значения токов в ветвях расчетной схемы, используя второй закон Кирхгофа. Прежде чем записать уравнения необходимо в схеме замещения обозначить направление токов и напряжений в расчетной схеме. Направление токов и напряжений расставим в соответствии с приведённой схемой (см. рис.2)
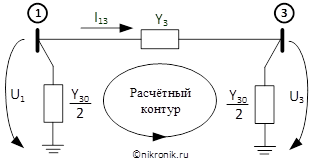
Рис.2. Ветви расчетной схемы
Значение тока в рассматриваемой ветви будет определяться в соответствии со следующим выражением:
где
и 
- комплексные значения фазного напряжения в начале и в конце рассматриваемой линии.
Значение перетока полной мощности в ветви будет определяться в соответствии со следующими выражениями:
- мощность в начале ветви: 
;
- мощность в конце ветви: 
.
В записанных выше формулах использовались следующие обозначения:
- и - комплексные значения фазного напряжения в начале и в конце рассматриваемой линии;
- 
- сопряженное значение тока в ветви.
В результате выполнения расчета установившегося режима электрической сети определяются значения векторов напряжения в узлах расчетной схемы, значения токов и перетоков активной и реактивной мощности в ветвях расчетной схемы.
