Рассмотрим однофазный двухобмоточный трансформатор (см. рис.1), который обладает собственными индуктивностями обмоток и взаимной индуктивностью между обмотками.
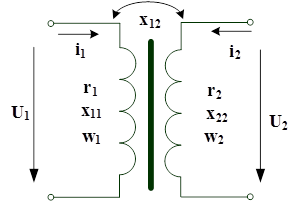
Рис.1. Схема однофазного двухобмоточного трансформатора
Для данной схемы однофазного двухобмоточного трансформатора можно записать систему уравнений, которая связывает напряжения и токи в обмотках трансформатора:
![]()
![]()
Записанная система уравнений содержит переменные, которые приведены к разным классам напряжения. Так, например, в первом уравнении содержаться переменные (сопротивления, токи и напряжения), которые приведены к обмотке с числом витков ![]() , а во втором уравнении содержаться переменные (сопротивления, токи и напряжения), которые приведены к обмотке с числом витков
, а во втором уравнении содержаться переменные (сопротивления, токи и напряжения), которые приведены к обмотке с числом витков ![]() . Данное обстоятельство затрудняет выполнение расчетов, количественного анализа процессов происходящих в трансформаторе и построение векторных диаграмм. Для упрощения анализа и расчета режимов работы трансформатора пользуются способом, при котором одна из его обмоток приводится к другой.
. Данное обстоятельство затрудняет выполнение расчетов, количественного анализа процессов происходящих в трансформаторе и построение векторных диаграмм. Для упрощения анализа и расчета режимов работы трансформатора пользуются способом, при котором одна из его обмоток приводится к другой.
Рассмотрим процесс приведение параметров трансформатора к числу витков первичной обмотке. Основной смысл приведения состоит в том, чтобы привести все переменные (сопротивления, токи и напряжения) к числу витков первичной обмотки, а электромагнитную связь между обмотками заменить электрической связью.
При выполнении приведения параметров трансформатора к числу витков первичной обмотке условно выполняют замену реальной вторичной обмотки некоторой фиктивной обмоткой с числом витков ![]() :
:
![]()
где коэффициент трансформации определяется по формуле ![]() .
.
Таким образом, коэффициент приведения вторичной обмотки к первичной равен коэффициенту трансформации. В дальнейшем все параметры приведенной обмотки будем обозначать со штрихами:
![]()
В приведенной обмотке в соответствии с новым числом витков увеличиваются все ЭДС, напряжения и падения напряжения, т.е.:
![]()
![]()
![]()
![]()
Важным условием приведения является то, чтобы мощности и потери энергии во вторичной обмотке не изменялись. Для этого должны выполняться равенства:
![]()
![]()
Аналогично последнему соотношению индуктивное сопротивление рассеяния приведенного трансформатора определяется следующим образом:
![]()
Перепишем систему уравнений через параметры приведенной обмотки.
› Первое уравнение перепишется в следующем виде
![]()
![]()
› Второе уравнение перепишется в следующем виде
![]()
![]()
![]()
Таким образом, система уравнений, записанная для приведенного трансформатора, будет иметь следующий вид:
![]()
![]()
где взаимное сопротивление приведенного трансформатора определяется по формуле
![]()
С учетом закона полного тока к системе уравнений можно добавить следующее уравнение:
![]()
В результате система уравнений преобразуется к виду:
![]()
![]()
Полученная система уравнений для приведенного трансформатора соответствует Т-образной схеме замещения однофазного двухобмоточного трансформатора (см. рис.2).
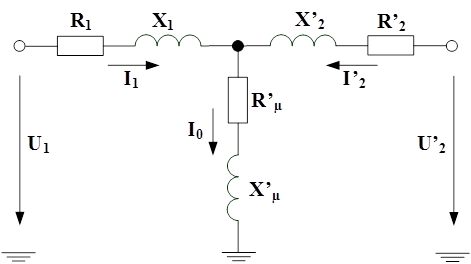
Рис.2. Схема замещения приведенного однофазного двухобмоточного трансформатора
В случае если в цепи вторичной обмотки расположены другие элементы (лини электропередач, нагрузка и т.д.) необходимо выполнить преобразование параметров данных элементов к числу витков первичной обмотки (или выполнить преобразование к одному классу напряжения). Так, например, полное сопротивление нагрузки, расположенная на стороне вторичной обмотки, будет преобразовываться следующим образом:
![]()