Развитие и совершенствование промышленного производства (энергетики, транспорта, машиностроения, космической техники и т.д.) требует внедрения современных систем управления, включая как автоматизированные (с участием человека-оператора), так и автоматические (без участия человека-оператора) системы управления.
Системы автоматического управления строятся на принципе обратной связи (см. рисунок 1), который заключается в том, что состояние объекта управления, характеризующиеся некоторыми параметрами 
, сравнивается в «управляющем устройстве» с заданным (желаемым) состоянием и в случае отличия текущего состояния от заданного в управляющем устройстве вырабатываются управляющие воздействия 
, которые возвращают состояние объекта к заданному. При этом отклонение состояние объекта от заданного вызывается возмущающими воздействиями 
.
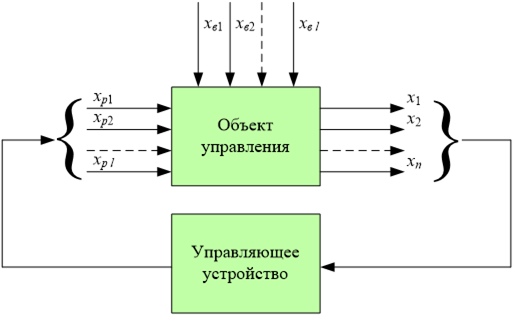
Рис.1. Система автоматического управления
Частным случаем систем автоматического управления являются системы автоматического регулирования, с помощью которых решается задача поддержания на определенном уровне или обеспечение изменения по заданному закону ограниченного числа параметров, характеризующих состояние объекта.
Степень совершенства решения задачи автоматического регулирования по отношению к исходным требованиям к ней определяются характеристиками объекта регулирования и характеристиками управляющего устройства (регулятора).
Поскольку характеристики объекта являются заданными, то необходимые требования к системе регулирования должны обеспечиваться соответствующим выбором характеристик регулятора.
В частных случаях совместно с системой регулирования по принципу обратной связи, который называют также системой регулирования по отклонению регулируемого параметра, применяется регулирование по возмущению.
Регулирование по возмущению заключается в том, что если между некоторыми возмущающими воздействиями и регулируемой величиной существует достаточно определенная связь, то можно, не дожидаясь появления отклонения, осуществлять воздействие на объект, препятствующее ожидаемому отклонению регулируемой величины.
Так как реальные объекты и элементы регулятора являются инерционными, то применение регулирования по возмущению в многих случаях позволяет повысить быстродействие системы регулирования, что бывает принципиально важным при решении многих задач управления и регулирования в энергетике.
П1. Понятие звена системы автоматического регулирования и математическое описание свойств линейных звеньев
Для анализа свойств систем автоматического регулирования используется их представления в виде структурной схемы, в которой отдельные элементы системы изображаются в виде звеньев, соединенных между собой в соответствии с соединением элементов, которые они замещают.
Отдельное звено характеризуется определенной математической связью между входной 
и выходной 
величинами (см. рисунок 2).
Рис.2. Звено системы автоматического регулирования
Звеньям системы предписывается свойство направленности действия, то есть способность одностороннего пропускания сигнала с входа на выход.
Связь между выходной и входной величинами линейного звена (или системы) выражается линейным дифференциальным уравнением с постоянными коэффициентами
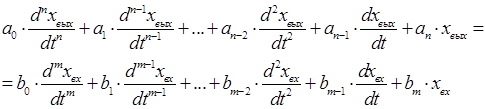
Решение данного линейного неоднородного дифференциального уравнения с постоянными коэффициентами относительно выходной величины может быть представлено в виде суммы частного решения этого уравнения и общего решения однородного дифференциального уравнения. Поэтому решение дифференциального уравнения в общем виде будет представлено суммой двух составляющих:
где
– свободная составляющая;
– вынужденная (принужденная) составляющая.
П.1. Первая составляющая 
определяется из общего решения однородного дифференциального уравнения, которое получается из дифференциального уравнения приравниванием его правой части к нулю. Общее решение однородного дифференциального уравнения характеризует так называемые свободные процессы, т.е. процессы, протекающие в схеме в отсутствие внешних источников энергии. Таким образом, характер свободных процессов не зависит от вида внешнего воздействия на цепь, а определяется только параметрами пассивных элементов и линейно управляемых источников, а также топологией схемы.
П.2. Вторая составляющая 
определяется как частное решении неоднородного дифференциального уравнения (правая часть не равна нулю). Частное решение уравнения определяет вынужденный режим работы, т.е. режим, задаваемый действующими в схеме независимыми источниками энергии.
П1.1. Передаточная функция звена
Как было показано ранее связь между выходной и входной величинами линейного звена (или системы) выражается линейным дифференциальным уравнением n-го порядка. Одним из способов решения дифференциальных уравнений (систем уравнений) с постоянными коэффициентами является метод интегральных преобразований, который позволяет функцию вещественной переменной (оригинал функции) заменить функцией комплексной переменной (изображение функции). В результате операции дифференцирования и интегрирования в пространстве функций-оригиналов преобразуются в алгебраическое умножение и деление в пространстве функций-изображений.
Передаточная функция основана на применении операторного метода, в частности преобразования Лапласа. Формула прямого преобразования Лапласа для некоторой функции времени x(t) имеет следующий вид
где p – оператор Лапласа (комплексное число).
Таким образом, Передаточная функция – это отношение операторного изображения выходной величины звена 
к операторному изображению входной величины 
при нулевых начальных условиях
Линейное дифференциальное уравнение n-го порядка можно переписать через изображение функции следующим образом:
Таким образом, передаточная функция будет определяться следующим образом:
П1.2. Переходная характеристика (или переходная функция)
Переходная функция h(t) – это закон изменения во времени выходной величины при изменении входной величины в виде единичной ступенчатой функции 1(t). Другими словами переходная характеристика показывает реакцию изменения выходного сигнала на единичное ступенчатое воздействие, приложенное к ее входу.
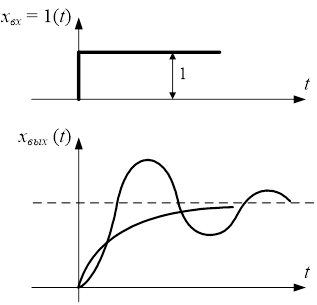
Рис.3. Переходная функция и реакция системы
Единичная ступенчатая функция описывается следующим образом
Cвязь между передаточной функцией и переходной функцией можно найти применив к функции 1(t) преобразование Лапласа
Следовательно, изображение переходной функции
При исследовании реального объекта переходную характеристику можно получить экспериментальным путем, подавая на его вход ступенчатое воздействие и фиксируя реакцию на выходе. Зная переходную характеристику, можно вычислить реакцию системы на произвольное входное воздействие.
П1.3. Импульсная переходная функции (весовая функция)
Импульсная переходная функция - это закон изменения во времени выходной величины при изменении входной величины в виде единичной импульсной функции 
. Другими словами, переходная характеристика показывает реакцию изменения выходного сигнала на единичное импульсное воздействие, приложенное к ее входу.
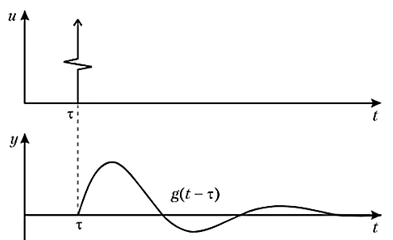
Рис.4. Импульсная переходная функция и реакция системы
Единичная импульсная функция описывается следующим образом
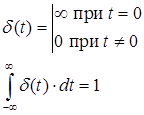
Связь между дельта-функцией и единичной ступенчатой функцией
Для линейных звеньев очевидно такая же связь будет иметь место между весовой функцией и переходной функцией
Следовательно, изображение по Лапласу весовой функции
Импульсная переходная функция позволяет вычислить реакцию системы на произвольное входное воздействие при нулевых начальных условиях
П1.4. Амплитудно-фазовая частотная характеристика (АФХ)
Амплитудно-фазовая частотная характеристика является важной динамической характеристикой объекта, которая определяет взаимосвязь между параметрами периодических сигналов на входе и выходе.
Таким образом, Амплитудно-фазовая частотная характеристика – это отношение комплексного изображения выходной величины к комплексному изображению входной, когда входная величина изменяется по гармоническому закону.
В качестве примера рассмотрим случай, когда на вход передаточной функции подается гармонический сигнал заданной амплитуды:
Комплексное изображение входного сигнала будет иметь следующий вид:
На выходе передаточной функции в установившемся режиме будет такой же гармонический сигнал той же частоты, но с другой амплитудой и со сдвигом по фазе:
Комплексное изображение выходного сигнала будет иметь следующий вид:
В соответствии с определением Амплитудно-фазовой частотной характеристики будет определяться как отношение комплексного изображения выходной величины к комплексному изображению входной
Следовательно, по определению АФХ, которая обозначается как 
, равна
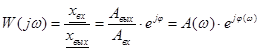
В полученном выражении функция 
и 
являются соответственно амплитудно-частотной и фазо-частотной характеристиками звена.
Выражение для амплитудно-фазовой характеристики, являющейся комплексной величиной, можно представить в алгебраической форме
В полученном выражении переменные 
и 
являются соответственно вещественная и мнимая частотные характеристики.
Амплитудно-фазовая характеристика однозначно связана с передаточной функцией.
Если учесть, что выражение для производной к-го порядка от 
и 
равны
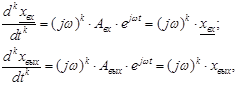
то при подстановке (18) в дифференциальное уравнение (9) получим
Амплитудно-фазовую характеристику можно получить подстановкой в выражение для передаточной функции.
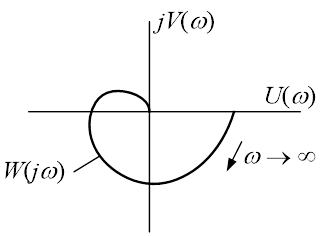
Рис.5. Амплитудно-фазовая характеристика
Для решения ряда практических задач анализа свойств систем автоматического регулирования амплитудно-фазовая характеристика строится на комплексной плоскости в виде годографа, который представляет из себя геометрическое место конца вектора 
при изменении частоты от 0 до 
(см. рисунок 5).
П1.5. Связь между входной и выходной величинами звена в установившемся режиме
Связь в установившемся режиме может быть получена, если в передаточной функции положить 
(все производные равны нулю).
Таким образом
Коэффициент 
называют коэффициентом усиления звена.
П1.6. Некоторые типовые звенья систем автоматического регулирования
П.1. Безинерционное звено – это звено в котором выходная величина воспроизводит без искажений и запаздываний входную величину. Связь между выходом и входом звена определяется алгебраическим уравнением.
Передаточная функция имеет следующий вид:
График переходной функция будет иметь следующий вид:
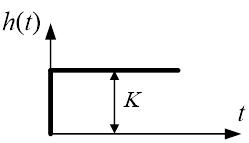
Рис.6. Переходная функция безинерционного звена
П.2. Идеальное дифференцирующее звено - это звено в котором выходная величина прямо пропорциональна скорости изменения входной величины.
Передаточная функция имеет следующий вид:
График переходной функция будет иметь следующий вид:
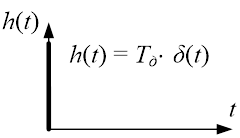
Рис.7. Переходная функция идеально дифференцирующего звена
Выходной сигнал этого звена пропорционален первой производной входного сигнала, т.е. тангенсу угла наклона вектора АФХ.
П.3. Реальное дифференцирующее звено – это звено в котором выходная величина зависит от скорости изменения входной величины.
Звено, описываемое дифференциальным уравнением
Преобразуя уравнение по Лапласу и определив отношение изображения выходной величины к входной, получим передаточную функцию. Передаточная функция имеет следующий вид:
График переходной функция будет иметь следующий вид:
Рис.8. Переходная функция дифференцирующего звена
П.4. Интегрирующее звено – это звено в котором выходная величина пропорциональна интегралу от входной величины.
Передаточная функция имеет следующий вид:
График переходной функция будет иметь следующий вид:
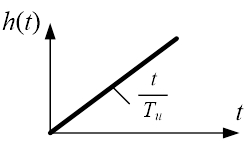
Рис.9. Переходная функция интегрирующего звена
П.5. Инерционное звено первого порядка – это апериодическое звено первого порядка, которое описывается дифференциальным уравнением.
Передаточная функция имеет следующий вид:
График переходной функция будет иметь следующий вид:
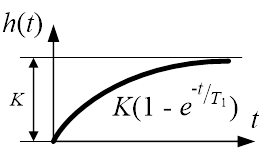
Рис.10. Переходная функция инерционного звена первого порядка
П.6. Инерционное звено второго порядка – это звено, зависимость между выходным и входным сигналами которого описывается дифференциальным уравнением второго порядка.
Передаточная функция имеет следующий вид:
В зависимости от значения корней характеристического уравнения инерционное звено второго порядка может быть: колебательным или апериодическим звеном второго порядка.
П.6.1. Колебательное звено второго порядка характеризуется комплексными корнями характеристического уравнения
Колебательным называется звено второго порядка, в котором при получении на входе ступенчатого воздействия, выходная величина стремится к новому установившемуся значению, совершая затухающие колебания.
График переходной функция будет иметь следующий вид:
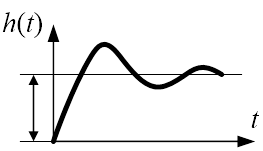
Рис.11. Переходная функция инерционного звена второго порядка (колебательное)
П.6.2. Апериодическое звено второго порядка характеризуется вещественными корнями характеристического уравнения
Апериодическим называется звено второго порядка, в котором при получении на входе ступенчатого воздействия, выходная величина стремится к новому установившемуся значению, совершая монотонное изменение.
График переходной функция будет иметь следующий вид:
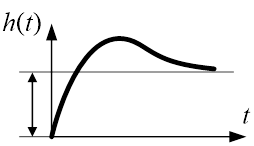
Рис.12. Переходная функция инерционного звена второго порядка (апериодическое)
Все представленные выше звенья можно разбить на две группы, принципиально отличающиеся по своим свойствам: статические звенья и астатические звенья.
П.1. Статические звенья – это такие звенья у которых в установившемся режиме между выходной и входной величинами имеется определенная связь. То есть эти звенья обладают свойством устойчивого равновесия. Из представленных звеньев к статическим относятся все звенья кроме интегрирующего.
Другими словами, система, в структуре которой нет последовательно присоединенного интегрирующего звена, называется статической. В статической системе при постоянном входном воздействии выходная величина со временем становится постоянной, принимая значение, отличное от первоначального.
П.2. Астатические звенья обладают безразличным равновесием (нейтральные звенья). Из представленных звеньев к астатическим относится интегрирующее звено. В установившемся режиме значение выходной величины может стремится к бесконечности.
Другими словами, система, в структуре которой есть последовательно присоединенное интегрирующее звено, называется астатической. В астатической системе при постоянном входном воздействии выходная величина непрерывно изменяется.
