Линия электропередачи (ЛЭП) — один из компонентов электрической сети, система энергетического оборудования, предназначенная для передачи электроэнергии посредством электрического тока.
Рассмотрим транспонированную линию электропередачи. Полный цикл транспозиции фаз позволяет усреднить собственные и взаимные индуктивные и емкостные сопротивления по всей длине линии электропередачи. Для транспонированной линии электропередачи схема замещения в фазной системе координат будет иметь следующий вид:
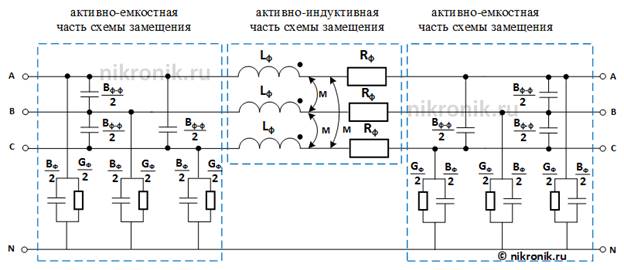
Рис.1. П-образная схема замещения трехфазной ЛЭП
Как видно схема замещения в фазной системе координат состоит из двух отдельных участков: первый участок отражает взаимодействие только магнитных полей (активно-индуктивная схема замещения), а второй участок расчетной схемы отражает электростатическое поле (активно-емкостная схема замещения).
Найдем схему замещения трехфазной линии электропередачи в системе координат прямой, обратной и нулевой последовательности. Система прямой последовательности представляет собой систему из трех векторов 
равных по модулю и повернутых друг относительно друга на угол 120 градусов по часовой стрелке. Система обратной последовательности представляет собой систему из трех векторов 
равных по модулю и повернутых друг относительно друга на угол 120 градусов против часовой стрелки. Система нулевой последовательности представляет собой систему из трех векторов 
равных по модулю и совпадающими по фазе.
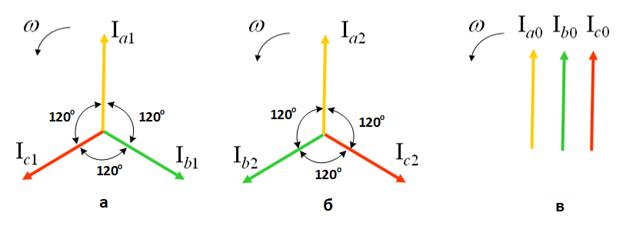
Рис.2. Система координат прямой (а), обратной (б) и нулевой (в) последовательности
Обозначения:
– система токов прямой последовательности;
– система токов обратной последовательности;
– система токов нулевой последовательности.
Любая несимметричная система 
может быть представлена через сумму трех симметричных систем (систему прямой, обратной и нулевой последовательности) следующим образом:
В матричной форме данное уравнение выглядит следующим образом:
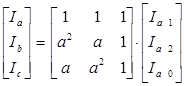
С другой стороны любая симметричная система (система прямой, обратной и нулевой последовательности) может быть представлена через несимметричную систему следующим образом:
В матричной форме данное уравнение выглядит следующим образом:
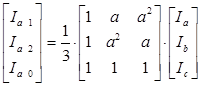
В представленных уравнениях используется оператор поворота «a», который представляет собой вектор единичной длины.
В случае умножения какого-либо вектора на оператор «a» происходит поворот исходного вектора без изменения его модуля на угол 120 градусов против часовой стрелки. В связи с этим для оператора «a» справедливы следующие соотношения:
Все приведенные соотношения справедливы для всех параметров электроэнергетического режима работы: для напряжений, токов и т.п.
Рассмотрим активно-индуктивную часть схемы замещения транспонированной линии электропередачи (рис.3).
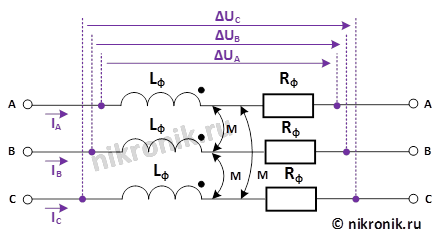
Рис.3. Активно-индуктивная часть схемы замещения трехфазной ЛЭП
Запишем систему уравнений, которая описывает процессы, происходящие в рассматриваемой части схемы замещения транспонированной линии электропередачи (первой участок полной схемы замещения):
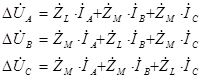
где собственное комплексное сопротивление линии электропередачи определяется по формуле
, а взаимное комплексное сопротивление определяется по формуле 
.
Перейдем от системы уравнений в фазной системе координат к системе уравнений, записанной для прямой, обратной и нулевой последовательности. Для этого умножим правую и левую части системы уравнений на матрицу преобразований, которая позволяет получить симметричную систему (система прямой, обратной и нулевой последовательности) через параметры фазной системы координат .
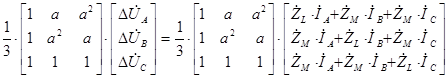
Первое слагаемое рассматриваемой системы перепишется в следующем виде:
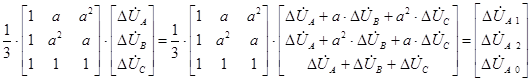
Второе слагаемое рассматриваемой системы перепишется в следующем виде:
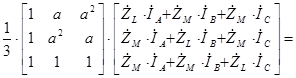
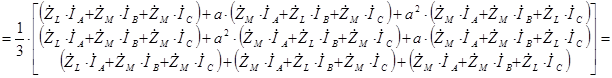
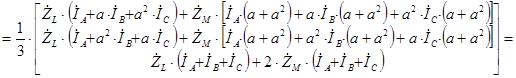
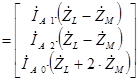
В результате полученная система уравнений может быть переписана в следующем виде:
где сопротивление прямой последовательности транспонированной линии электропередачи определяется по формуле 
, а сопротивление нулевой последовательности транспонированной линии электропередачи определяется по формуле 
. Таким образом, сопротивление прямой, обратной и нулевой последовательности линии электропередачи определяются из собственного и взаимного сопротивления линии электропередачи.
Усредненные значения соотношений между сопротивлениями прямой и нулевой последовательностей для воздушных линий электропередачи представлен в таблице №1.
Таблица №1. Соотношение между сопротивлениями прямой и нулевой последовательности воздушной линии электропередач.
|
Характеристика линий |
Отношение X0/X1 |
|
Одноцепная линия без грозозащитных тросов |
3,5 |
|
Одноцепная линия со стальными тросами |
3,0 |
|
Одноцепная линия с хорошо проводимыми тросами |
2,0 |
|
Двухцепная линия без грозозащитных тросов |
5,5 |
|
Двухцепная линия со стальными тросами |
4,7 |
|
Двухцепная линия с хорошо проводимыми тросами |
3,5 |
Рассмотрим активно-емкостную часть схемы замещения транспонированной линии электропередачи (рис.4).
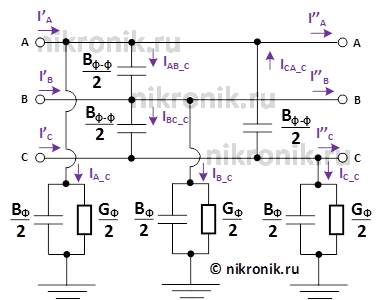
Рис.4. Активно-емкостная часть схемы замещения трехфазной ЛЭП
Запишем систему уравнений, которая описывает процессы, происходящие в рассматриваемой схеме замещения транспонированной линии электропередачи (второй участок полной схемы замещения):
∙ По второму закону Кирхгофа запишем следующую систему уравнений:
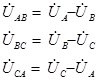
∙ По первому закону Кирхгофа запишем следующую систему уравнений:
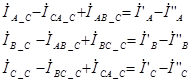
В результате система уравнений, которая описывает процессы, происходящие в рассматриваемой части схемы замещения транспонированной линии электропередачи, записывается в следующем виде:
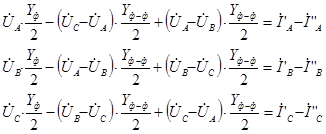
Сгруппируем переменные представленной системы уравнений.
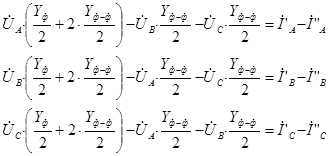
Перейдем от системы уравнений в фазной системе координат к системе уравнений, записанной для прямой, обратной и нулевой последовательности. Для этого умножим правую и левую части системы уравнений на матрицу преобразований, которая позволяет получить симметричную систему (система прямой, обратной и нулевой последовательности) через параметры фазной системы координат .
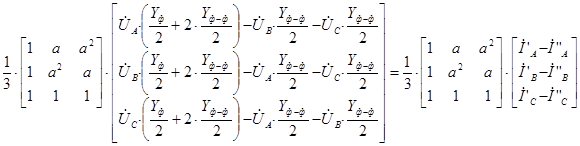
В результате преобразования системы уравнений записанной в фазной системе координат получим следующую систему для токов и напряжений прямой, обратной и нулевой последовательности.
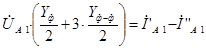
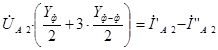
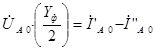
Таким образом, получили выражения, которые позволяют определить проводимости на землю для прямой, обратной и нулевой последовательности транспонированной трехфазной линии электропередач:
Представленная система уравнений соответствует следующим схемам замещения транспонированной трехфазной линии электропередачи в системе координат прямой, обратной и нулевой последовательности.
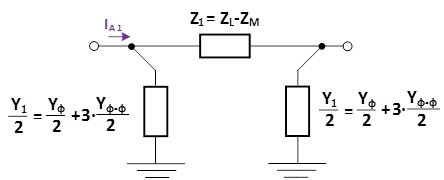
Рис.5. Схема замещения трехфазной ЛЭП в системе координат прямой последовательности
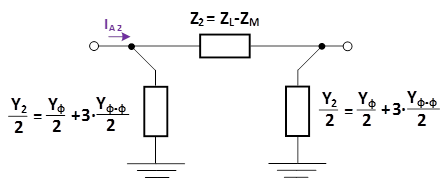
Рис.6. Схема замещения трехфазной ЛЭП в системе координат обратной последовательности
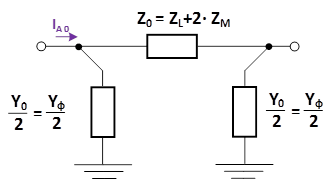
Рис.7. Схема замещения трехфазной ЛЭП в системе координат нулевой последовательности
В результате схемы замещения транспонированной линии электропередачи в системе координат прямой, обратной и нулевой последовательности представляют собой П-образные схемы замещения. Следует отметить, что представленные схемы замещения не имеют взаимных сопротивлений (междуфазных емкостей и взаимных индуктивностей), соответственно данная особенность облегчает выполнение расчетов по данным схемам замещения и позволяет решать задачи в однофазной постановке.
Моделирование воздушной линии электропередач в фазной системе координат через параметры прямой, обратной и нулевой последовательности
Выполним обратное преобразование и найдем систему уравнений в фазной системе координат, которая описывает процессы, происходящие в рассматриваемой схеме замещения транспонированной линии электропередачи через параметры прямой, обратной и нулевой последовательности.
Рассмотрим активно-индуктивную часть схемы замещения транспонированной линии электропередачи. Для выполнения обратного преобразования умножим правую и левую части системы уравнений, записанной для прямой, обратной и нулевой последовательности, на матрицу преобразований.
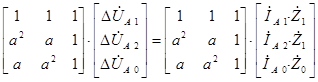
В результате преобразования получим следующую систему уравнений с учетом взаимосвязи между током нулевой последовательности и током в нейтрале 
.
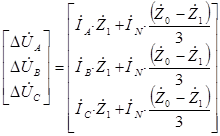
Рассмотрим активно-емкостную часть схемы замещения транспонированной линии электропередачи. Для выполнения обратного преобразования умножим правую и левую части системы уравнений, записанной для прямой, обратной и нулевой последовательности, на матрицу преобразований.
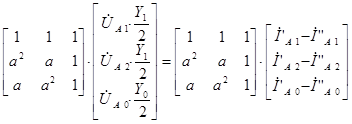
В результате преобразования получим следующую систему уравнений с учетом взаимосвязи между напряжением нулевой последовательности и напряжением в нейтрале 
.
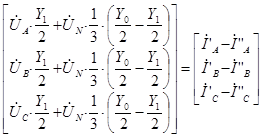
Представленная система уравнений соответствует следующей схеме замещения транспонированной трехфазной линии электропередачи в фазной системе координат.
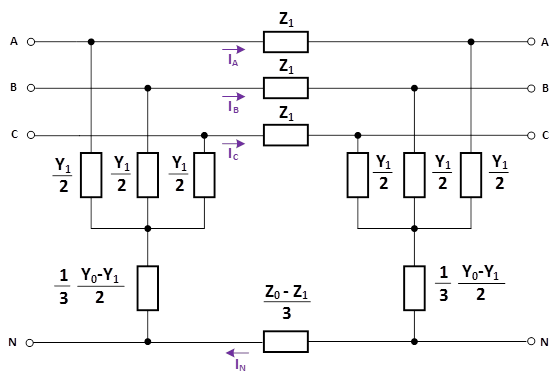
Рис.8. Схема замещения трехфазной ЛЭП в системе фазной системе координат
Данная схема замещения позволяет выполнять в фазной системе координат расчеты различных режимов работы: расчет установившегося режима работы, расчеты симметричных и несимметричных коротких замыканий (поперечная несимметрия), а также расчеты обрывов фаз линии электропередачи (продольная несимметрия).
