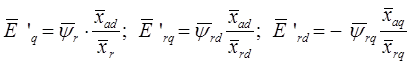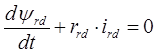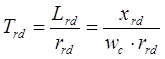Система относительных единиц
Система уравнений синхронной машины обычно записывается в относительных единицах, вследствие чего упрощается запись данных уравнений и облегчается сравнение результатов исследования переходных процессов для машин различной мощности.
Система относительных единиц — способ расчета параметров в системах передачи электроэнергии, при котором значения системных величин (напряжений, токов, сопротивлений, мощностей и т.п.) выражаются как множители определенной базовой величины, принятой за единицу.
Существует несколько видов систем относительных единиц, основные из которых: система относительных единиц Горева и система относительных единиц «Xad». В рамках данной публикации будем рассматривать систему относительных единиц Горева.
Базисные величины статорной цепи
В качестве независимых базисных величин для статорной цепи обычно принимается амплитуда номинальных тока и фазного напряжения, синхронная угловая частота 
.
Базисные значения тока и напряжения статора (контуров якоря) машины равны амплитуде фазного тока и фазного напряжения:
, 
Базисное значение мощности статорной цепи будет определяться в следующем виде:
Базисное значение угловой скорости равно синхронной угловой скорости при номинальной частоте:
эл. радиан/сек.
Прочие базисные параметры определяются по следующим соотношениям:
; 
; 
Базисные величины роторной цепи
В качестве независимых базисных величин для роторной цепи принимается такие значения тока, напряжения и потокосцепления роторного контура, которые обусловливают на статоре идеализированной синхронной машины в режиме холостого хода номинальное напряжение.
При протекании базисного тока по роторному контуру (обмотка ротора или демпферные обмотки) в режиме холостого хода при синхронной угловой скорости напряжение статора равно номинальному. Данное утверждение записывается в следующем виде:
; 
; 
.
Базисные напряжения роторных контуров определяются как произведение базисного тока на активное сопротивление контуров:
; 
; 
.
Базисные значения сопротивлений роторных контуров принимаются равными активным сопротивлениям контуров:
; 
; 
.
Представленный подход позволяет легко связать базисные величины статорной цепи базисными величинами роторной цепи.
Определение величины базисного тока ротора и демпферных обмоток.
Базисное значение тока обмотки возбуждения определяется по спрямленной в начале координат характеристике холостого хода машины (см. рис.1), построенной в относительных единицах.
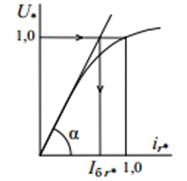
Рис.1. Определение базисного значения тока роторных контуров.
Ток возбуждения отнесен к номинальному току возбуждения на холостом ходе:
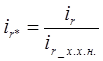
где 
- это такой ток возбуждения, при котором на холостом ходе генератора при номинальной угловой скорости вращения напряжение на выводах обмотки статора равно номинальному значению.
Графическое определение базисного тока 
, выраженного в долях 
, показано стрелками на рис., базисный ток в именованных единицах определяется по формуле 
. Если характеристика холостого хода задана в виде таблицы пар значений 
, 
, можно найти тангенс угла наклона начального участка характеристики и вычислить:
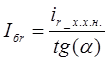
Базисные значения токов демпферных контуров в осях d и q равны:
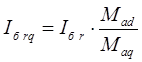
Преобразим систему уравнений явнополюсной синхронной машины в систему относительных единиц Горева.
Система уравнений для напряжений статорной цепи
Рассмотрим систему уравнений, которая записана для статорной цепи.
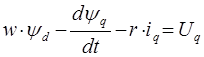
Перепишем данную систему уравнений относительно базисных переменных, для этого разделим представленные уравнения на базисное значение напряжения:
.
Первое уравнение рассматриваемой системы преобразуется к следующему виду:
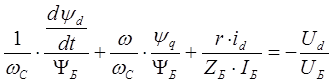
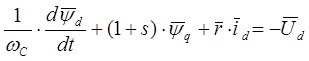
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
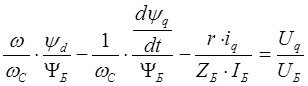
где s - скольжение ротора относительно синхронной оси.
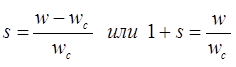
Скольжение - Относительная разность скоростей поля статора и ротора называется скольжением
Скольжение не может быть равным нулю, так как при одинаковых скоростях поля и ротора прекратилось бы наведение токов в роторе и, следовательно, отсутствовал бы электромагнитный вращающий момент.
Скольжение асинхронного генератора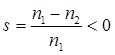 
.
Система уравнений для потокосцеплений статорных контуров
Рассмотрим систему уравнений, которая записана для потокосцеплений статорных контуров.
Для выполнения дальнейших преобразований системы уравнений введем новые переменные:
› синхронная ЭДС статора 
- ЭДС, индуктируемая в контуре статора током возбуждения при синхронной частоте вращения:
› синхронная ЭДС, связанные с токами демпферных контуров 
по поперечной оси:
› синхронная ЭДС, связанные с токами демпферных контуров 
по продольной оси:
C учетом новых введенных переменных система уравнений перепишется в следующем виде:
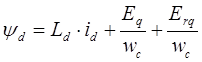
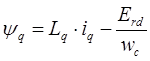
Перепишем систему уравнений относительно базисных переменных, для этого разделим данные уравнения на базисный поток статорной цепи:
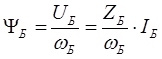
Первое уравнение рассматриваемой системы преобразуется к следующему виду:
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
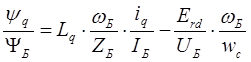
где синхронное индуктивное сопротивление машины по продольной оси 
в относительных единицах определяется следующим образом:
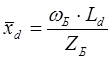
синхронное индуктивное сопротивление машины по поперечной оси 
в относительных единицах определяется следующим образом:
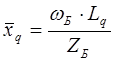
Система уравнений для потокосцеплений роторных контуров
Рассмотрим систему уравнений, которая записана для потокосцеплений роторных контуров.
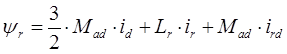
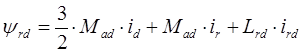
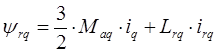
Умножим данную систему уравнений на выражение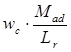 
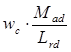(или 
; или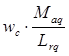 
) и введем новые переменные в систему уравнений:
› переходная ЭДС статора 
:
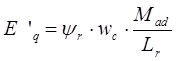
› переходная ЭДС, связанная с токами демпферных контуров 
по поперечной оси:
› переходная ЭДС, связанная с токами демпферных контуров 
по продольной оси:
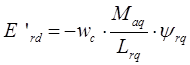
В результате преобразования получим следующую систему уравнений для потокосцеплений роторных контуров.
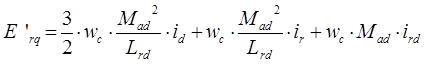
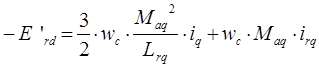
Перепишем данную систему уравнений через сопротивления 
, 
, 
, 
и 
. В результате данного преобразования получим следующую систему уравнений:
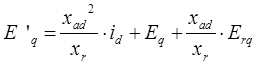
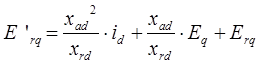
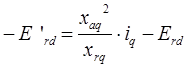
где
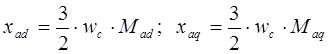
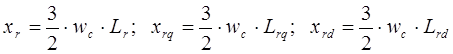
Перепишем систему уравнений относительно базисных переменных, для этого разделим данные уравнения на базисное напряжение статорной цепи:
В результате данного преобразования получим следующую систему уравнений (в относительных единицах):
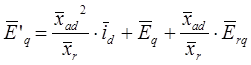
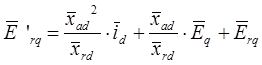
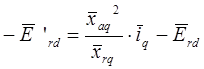
Система уравнений для напряжений роторной цепи
Рассмотрим систему уравнений, которая записана для роторных цепей.
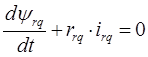
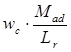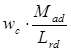Умножим данную систему уравнений на выражение (или 
или ).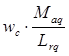
Первое уравнение рассматриваемой системы преобразуется к следующему виду:
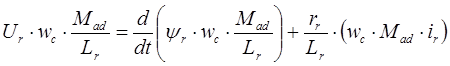
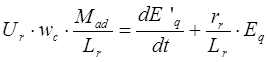
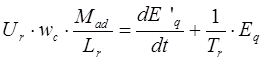
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
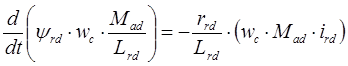
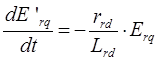
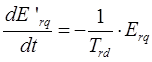
Третье уравнение рассматриваемой системы преобразуется к следующему виду:
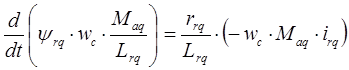
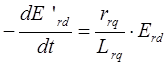
Постоянные времени используемые в уравнениях определяются следующим образом:
› Постоянная времени контура возбуждения
:
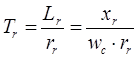
› Постоянные времени демпферных контуров
:
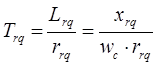
Перепишем полученную систему уравнений относительно базисных переменных, для этого разделим данные уравнения на базисное напряжение:
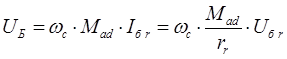
Первое уравнение рассматриваемой системы преобразуется к следующему виду:
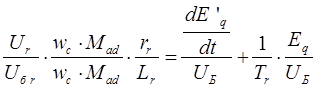
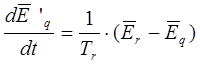
где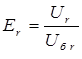 
в относительных единицах.
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
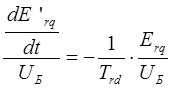
Третье уравнение рассматриваемой системы преобразуется к следующему виду:
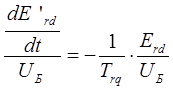
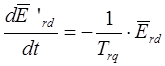
Система уравнений явнолюполюсной синхронной машины в относительных единицах Горева
В результате преобразования была получена система уравнений явнолюполюсной синхронной машины для вращающейся системы координат (odq) с учетом демпферных контуров, которая представлена в относительных единицах Горева.
1. Система уравнений для напряжений статорной цепи:
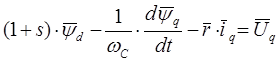
2. Система уравнений для потокосцеплений статорных контуров:
3. Система уравнений для потокосцеплений роторных контуров:
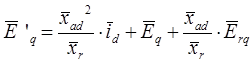
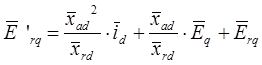
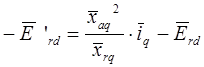
4. Система уравнений для напряжений роторной цепи и демпферных контуров (уравнения равновесия напряжений роторных контуров):
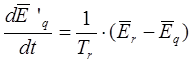
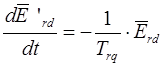
В систему уравнений, которая записана в относительных единицах Горева, входят переменные статорной цепи и переменные обмотки ротора:
› Переменные статорной цепи
Переменные 
, 
, 
, 
, 
, 
, 
, 
записаны относительно базисного напряжения статорной цепи;
Переменные 
, 
, 
, 
записаны относительно базисного тока и потокосцепления статорной цепи.
› Переменные обмотки ротора
Переменные 
записаны относительно базисного напряжения ротора;
Переменные 
, 
, 
записаны относительно базисного тока ротора.
Сопротивления, которые входят в систему уравнений синхронной машины
Ниже представлены сопротивления, которые входят в представленную систему уравнений синхронной машины (в именованных единицах).
- синхронное индуктивное сопротивление машины по продольной оси;
- синхронное индуктивное сопротивление машины по поперечной оси;
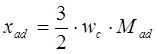- индуктивное сопротивление реакции якоря по продольной оси (сопротивление взаимоиндукции роторных и статорных контуров в продольной оси)
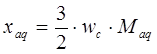- индуктивное сопротивление реакции якоря по поперечной оси (сопротивление взаимоиндукции роторных и статорных контуров в поперечной оси)
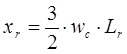- индуктивное сопротивление обмотки возбуждения
- индуктивное сопротивление демпферной обмотки в продольной оси
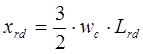- индуктивное сопротивление демпферной обмотки в поперечной оси
- индуктивное сопротивление рассеяния
Примечание:
Для перевода данных переменных сопротивления к базисным единицам достаточно разделить переменные на базисную величину 
.
Соотношения между переменными 
и , 
и 
:
Вспомогательные ЭДС, которые входят в систему уравнений синхронной машины
Ниже представлены вспомогательные ЭДС, которые входят в представленную систему уравнений синхронной машины (в именованных единицах).
- синхронная ЭДС статора, которая индуктируется током возбуждения в контуре статорной обмотке при синхронной частоте вращения.
- синхронная ЭДС, связанные с токами демпферных контуров
- синхронная ЭДС, связанные с токами демпферных контуров
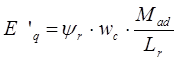- переходная ЭДС статора синхронной машины
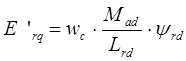- переходная ЭДС, связанная с токами демпферных контуров
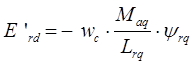- переходная ЭДС, связанная с токами демпферных контуров
Примечание:
Для перевода переменных из именованных единиц к базисным единицам достаточно разделить переменные на базисную величину напряжения:
.
Таким образом, вспомогательные ЭДС в относительных единицах Горева определяются следующим образом:
