Методы моделирования основной кривой намагничивания

Процессы, происходящие в силовых и измерительных трансформаторах, описываются системой уравнений, составленной для электрической и магнитной цепи. Магнитная цепь представляет собой сердечник, в котором замыкается магнитный поток, создаваемый магнитодвижущей силой.  Для уменьшения активных потерь из-за образования вихревых токов сердечники электротехнических устройств составляют их шихтованных листов ферромагнитного материала. Под действием внешнего магнитного поля (H), созданного током в катушке, наложенной на стальной магнитопровод, происходит процесс ориентации доменов в магнитопроводе и смещение их границ. Это приводит к намагничиванию (M) стального магнитопровода, причем намагниченность увеличивается с увеличением внешнего магнитного поля.  Зависимость намагниченности материала от напряжённости магнитного поля M(H) (или B(H)) называется кривой намагничивания (magnetization curve), которая обычно представлены исследователю в виде формул, графиков или таблиц. Также следует отметить, что ферромагнитный материала обладает способностью сохранять намагниченность в отсутствии внешнего магнитного поля.

При намагничивании предварительно размагниченного образца различают следующие типы зависимостей (кривых намагничивания):

1. Начальная кривая намагничивания – это зависимость, которую получают при монотонном увеличении напряженности магнитного поля (Н);

2. Безгистерезисная (идеальную) кривая намагничивания – это зависимость, которую получают при одновременном действии постоянного поля и переменного поля с убывающей до нуля амплитудой.

3. Основная кривая намагничивания, представляющая собой геометрическое место вершин симметричных петель гистерезиса, получающихся при циклическом перемагничивании.

Начальная кривая намагничивания зависит от случайных причин, например от механических сотрясений, колебаний температуры, характера изменения намагничивающего поля и т.д. Следовательно, начальная кривая намагничивания не может быть использована для сравнительной оценки свойств различных материалов.

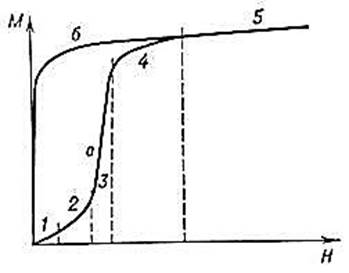
Рис.1. Основная кривая намагничивания (а) и безгистерезисная кривая намагничивания (б).

Основная кривая намагничивания, напротив, является важнейшей характеристикой магнитных материалов, которая не подвержена внешним факторам. Основная кривая намагничивания обычно мало отличается от начальной кривой намагничивания, но не совпадает с ней. Основная кривая намагничивания представляет собой геометрическое место вершин петель гистерезиса, полученных при циклическом перемагничивании (см. рис. 2) и отражает изменение магнитной индукции (В) от напряженности магнитного поля (Н), которое создается в материале при намагничивании. Для получения основной кривой намагничивания снимается ряд петель гистерезиса для различных токов.

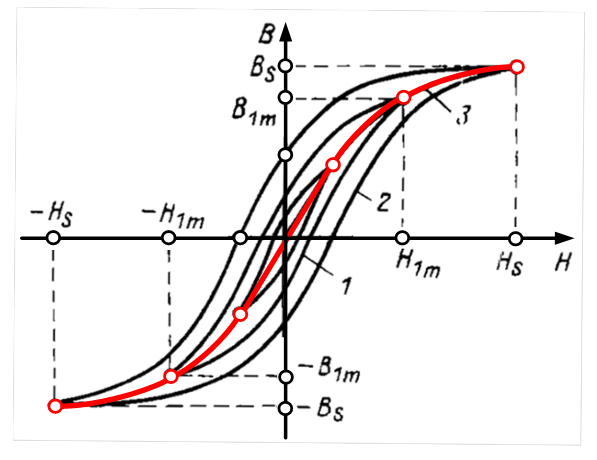
Рис.2. Симметричные циклы магнитного гистерезиса и основная кривая намагничивания

Основная кривая намагничивания используется при технических расчетах магнитных цепей, когда требуется исследовать (моделировать) нелинейные индуктивные элементы. Основная кривая намагничивания представлена в виде зависимости магнитной индукции от напряженности магнитного поля B(H) или обратной функциональной зависимостью H(B). На основной кривой намагничивания принято различать три участка: начальный, соответствующий нижнему колену кривой,  второй участок соответствует быстрому возрастанию индукции и третий участок соответствует насыщению стали сердечника.

В качестве примера представим в табличной форме кривую намагничивания стали 2312, которая имеет следующую зависимость:

Аналитические выражения для описания основной кривой намагничивания

Существуют множество способов аппроксимации таблично заданной функции аналитической функцией, которая с определенной степенью точности моделирует исходную функцию в заданных точках. Данные математические способы описания таблично заданной функции строятся на применении различных математических функций. Следует отметить, что логарифмическая и экспоненциальная аппроксимации ограничены задачами расчета магнитных цепей с постоянными полями, поэтому при исследовании процессов в переменном магнитном поле использование данных функций аппроксимации нерационально. Данное ограничение связано с тем, что получаемые кривые намагничивания несимметричны относительно начала координат и поэтому могут быть использованы только в случае постоянного магнитного поля (H и B не меняют знака).

Моделирование основной кривой намагничивания с помощью аналитической функции позволяет с высокой точностью описать реальную кривую намагничивания на всех характерных участках, задать кривую намагничивания непрерывной функцией, что позволяет избежать изломов и разрывов экстремальных зависимостей, получаемых в результате дифференцирования. В целом широкое применение имеют степенные функции, так как они позволяют выполнять расчеты магнитных цепей с переменными магнитными полями. Точность аппроксимации реальной кривой степенным полиномом пропорциональна количеству определения его коэффициентов. Функции гиперболических синуса и тангенса при разложении в ряд превращаются в степенные полиномы. Результаты аппроксимации гиперболическими синусом и тангенсом близки к аппроксимации степенным полиномом, и во многих случаях имеют достаточно точное совпадение с данными натурных экспериментов. Широкое распространение получило применение арктангенсных функций аппроксимации кривых намагничивания нелинейных индуктивных элементов, поскольку как саму функцию, так и ее производную исчисляют сравнительно просто при достаточной точности отображения оригинальной кривой, поэтому для дальнейших исследований в качестве модели была применена арктангенсная функция аппроксимации с тремя коэффициентами и линейным членом.

1. Аппроксимация кривой намагничивания с помощью степенного полинома

Аппроксимация степенным полиномом является нечетной функцией и может быть использована для расчета магнитных цепей как с постоянным, так и с переменным полем. Основная кривая намагничивания может описываться с помощью нечетного степенного полинома следующего вида:

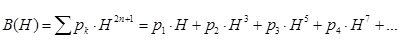
или

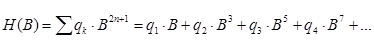
где n - число учитываемых членов ряда;

k - постоянные коэффициенты ряда;

p1, …, p4 и q1, …, q4 – это коэффициенты, которые определяются путем полиномиальной регрессии по методу наименьших квадратов.

Таким образом, коэффициенты определяются в зависимости от исходной кривой намагничивания. Следует отметить, что чем больше степень слагаемых (степень) полинома, тем лучше совпадает расчётные и реальная кривая намагничивания.

Коэффициенты полинома n-степени определяются по методу наименьших квадратов. В соответствии с данным методом коэффициенты аппроксимирующей функции определяется из условия минимума суммы квадратов отклонений  расчетной аппроксимирующей функции от заданного массива экспериментальных данных.

Наименьший порядок степенного полинома для аппроксимации кривой намагничивания приемлемой точности должен быть равен семи. Соответственно, условие минимума по методу наименьших квадратов для полинома седьмой степени записывается в виде следующего выражения: 

 Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным p1, p2, p3 и p4 (коэффициентам полинома). В результате дифференцирования получим следующую систему уравнений:

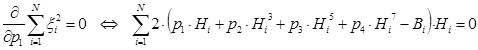
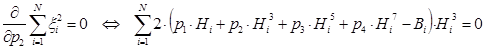
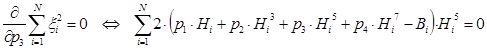
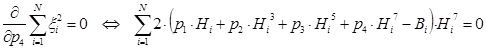
Решение данной нелинейной системы уравнений позволит определить коэффициенты аппроксимирующей функции.

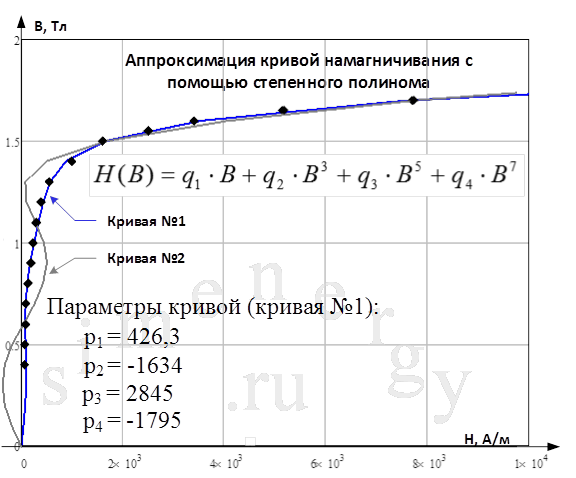
Рис.3. Аппроксимация кривой намагничивания с помощью функции степенного полинома

Основным недостатком является большое количество коэффициентов и относительно высокий порядок аппроксимирующего полинома, который позволяет получить приемлемую точность аппроксимации кривой намагничивания. Также следует отметить, что при подборе неизвестных коэффициентов аппроксимирующей кривой по методу наименьших квадратов для обеспечения требования условия минимума суммы квадратов отклонений для больших индукций получим зигзагообразную кривую намагничивания для маленьких индукций (см. кривую №2). Другими словами при использовании степенного полинома необходимо дополнительно анализировать монотонность получаемой кривой намагничивания. Использование полученной «зигзагообразной» кривой намагничивания приведет заведомо к неправильным результатам расчета.

2. Аппроксимация кривой намагничивания функцией гиперболического синуса

В соответствии с данным способом основная кривая намагничивания аппроксимируется гиперболической функцией синуса, которая содержит два настраиваемых коэффициента.

Неизвестные коэффициенты (p1 и p2) могут быть определены по методу наименьших квадратов. Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений  расчетной аппроксимирующей функции от заданного массива экспериментальных точек. Данный критерий метода наименьших квадратов записывается в виде следующего выражения: 

 Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным p1 и p2. В результате получим следующую систему уравнений:

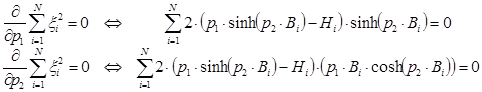
Решение данной нелинейной системы уравнений позволит определить коэффициенты аппроксимирующей функции.

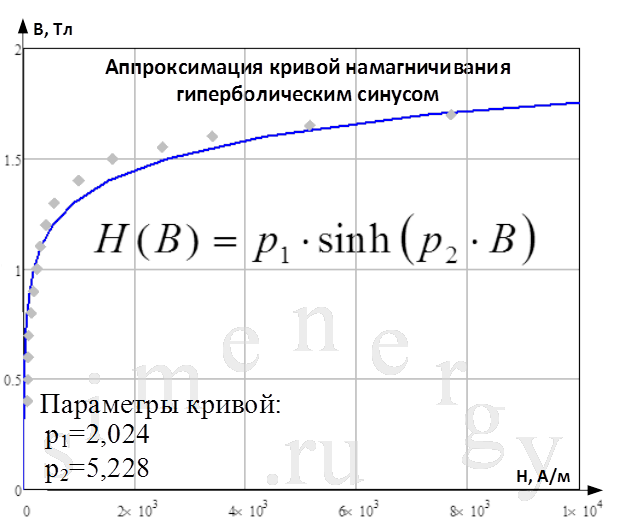
Рис.4. Аппроксимация кривой намагничивания функцией гиперболического синуса

Следует отметить, что для описания кривой намагничивания можно также  использовать гиперболическую функцию синуса, которая содержит три настраиваемых коэффициента:

Данная аппроксимация является нечетной и может быть использована для расчета магнитных цепей как с постоянным, так и с переменным полем.

3. Аппроксимация кривой намагничивания функцией гиперболического тангенса

В соответствии с данным способом основная кривая намагничивания аппроксимируется гиперболической функцией тангенса, которая содержит три настраиваемых коэффициента.

Неизвестные коэффициенты (p1, p2 и p3) могут быть определены по методу наименьших квадратов. Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений  расчетной аппроксимирующей функции от заданного массива экспериментальных точек. Данный критерий метода наименьших квадратов записывается в виде следующего выражения: 

 Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным p1, p2 и p3. В результате получим следующую систему уравнений:

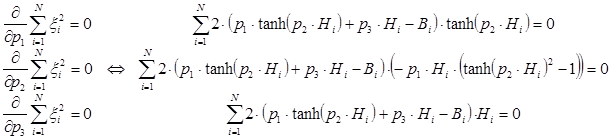
Решение данной нелинейной системы уравнений позволит определить коэффициенты аппроксимирующей функции.

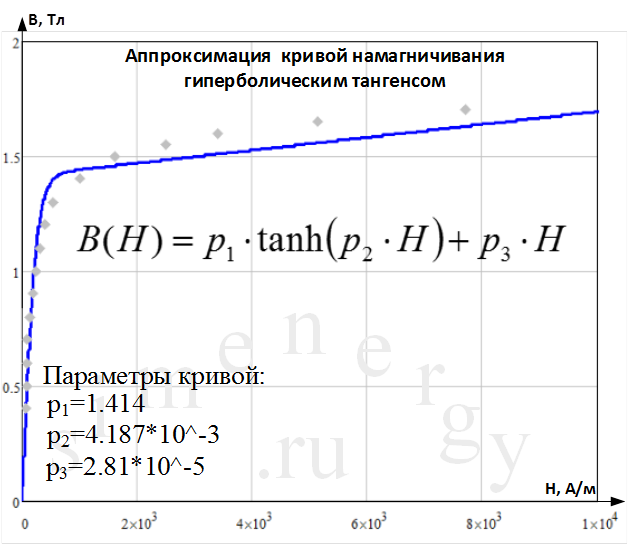
Рис.5. Аппроксимация кривой намагничивания функцией гиперболического тангенса

Данная аппроксимация является нечетной и может быть использована для расчета магнитных цепей как с постоянным, так и с переменным полем.

4. Аппроксимация кривой намагничивания функцией арктангенса

Широкое распространение получило применение арктангенсных функций аппроксимации кривой намагничивания из-за простоты вычислений самой функции и ее производной, а также достаточной точности отображения оригинальной кривой намагничивания.

В соответствии с данным способом основная кривая намагничивания аппроксимируется функцией с арктангенсом с линейным членом, которая содержит три настраиваемых коэффициента.

Неизвестные коэффициенты (p1, p2 и p3) могут быть определены по методу наименьших квадратов. Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений  расчетной аппроксимирующей функции от заданного массива экспериментальных точек. Данный критерий метода наименьших квадратов записывается в виде следующего выражения: 

 Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным p1, p2 и p3. В результате получим следующую систему уравнений:

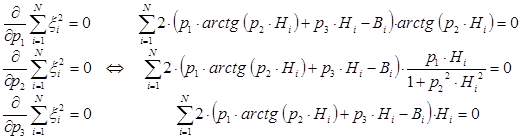
Решение данной нелинейной системы уравнений позволит определить коэффициенты аппроксимирующей функции.

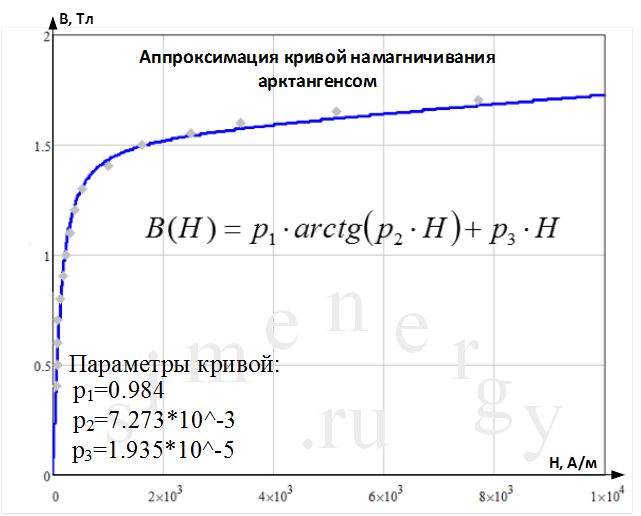
Рис.6. Аппроксимация кривой намагничивания функцией арктангенса

Данная аппроксимация является нечетной и может быть использована для расчета магнитных цепей как с постоянным, так и с переменным полем.

5.Аппроксимация кривой намагничивания с помощью сплайн-функций

При наличии значительного количества экспериментальных точек и высоких требованиях к точности аппроксимации довольно эффективным является метод сплайнов, заключающийся в использовании на выбранных участках кривой намагничивания разных сплайн-функций. Результирующая аппроксимирующая сплайн-функция представляет собой совокупность  кривых, которые описываются функциями, содержащие несколько коэффициентов. При этом коэффициенты определяются таким образом, чтобы в точках стыковки непрерывна была не только сама результирующая сплайн-функция, но и некоторое число ее производных. Таким образом, сплайн-функция позволяет довольно четко описывать кривые намагничивания различных материалов.

Сплайн-функция может быть образована различными типами функций, но на практике принято разделять сплайн-функции на три группы:

- кубический сплайн (функция cspline)

- параболический сплайн (функция pspline)

- линейный сплайн (функция lspline)

Используя большее количество участков аппроксимации и экспериментальных точек, снижается погрешность расчета, но при этом увеличивается число уравнений, которые требуют совместного решения. В большинстве случаев для построения аппроксимирующего сплайна используют ряд математических пакетов (MathCAD и MATLAB), имеющий в своем составе встроенный сплайн аппарат, подбирающий функции наилучшим образом. Одним из основных недостатков сплайн-аппроксимации является отсутствие одного выражения для всей кривой, так как используется набор сплайн-функций для различных интервалов между узловыми точками.