Угловая характеристика мощности синхронной машины

Рассмотрим простейшую схему электропередачи, состоящую из генератора электростанции, повышающего трансформатора, линии электропередачи и шин приемной системы. Введем допущение о том, что приемная система обладает бесконечной  мощностью, так что любое изменение режима рассматриваемой электропередачи не вызовет изменения напряжения на шинах приемной системы и частоты. Дополнительно к выше написанному допущению пренебрежем активным сопротивлением элементов электропередачи, емкостью линии и токами намагничивания трансформаторов.

Рис.1. Расчетная схема

Режим работы генератора в установившемся режиме работы описывается следующим уравнением:

,

где  - вспомогательная ЭДС;

- синхронная ЭДС статора.

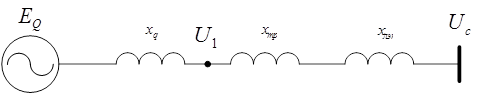
Рис.2. Схема замещения расчетной цепи

Построим векторную диаграмму для соответствующей схемы замещения.

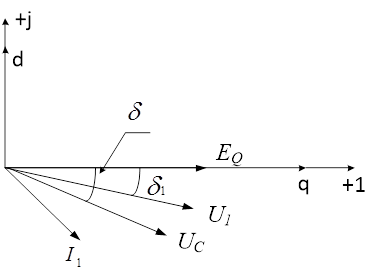
Рис.3. Векторная диаграмма

При выполнении расчетом в дальнейшем за вещественную ось выбрана ось q, а за мнимую - ось d.

Полная электрическая мощность выдаваемая в сеть от генератора определяется по формуле:

     (о.е.)

Примечание: В именованных единицах формулы для определения мощности выглядит следующим образом: (и.е.), однако при выводе последующих формул используется формула , которая связывает параметры в относительных единицах. В качестве базисных величин выбраны следующие переменные: линейное напряжение и фазный ток. В результате при переводе формулы из именованных единиц в относительные единицы получим запись: (о.е.).

Преобразуем формулу для определения полной мощности к зависимости передаваемой мощности от параметров схемы замещения, значений напряжений в узлах расчетной схемы и взаимного угла между векторами напряжения (δ).

Ток, который передается от генератора можно определить исходя из второго закона Кирхгофа:

,

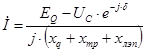где .

Подставляю в формулу для мощности выражение для определения сопряженного тока, получим следующую запись:

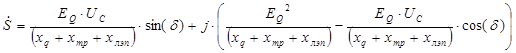
В результате после преобразования была получена формула для определения активной и реактивной мощности от режимных параметров. Рассмотрим выражение для определения активной мощности:

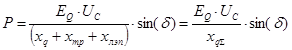
В полученное выражение для мощности входит переменная , которая не имеет физического смысла. В зависимости от исходной системы возбуждения генератора последнее выражение переписывается в различных формах в зависимости от принятых исходных условий:

- постоянство синхронной ЭДС статора ();

- постоянство потокосцепления контура возбуждения ( );

- постоянное напряжение на зажимах генератора ( ).

а. Угловая характеристика мощности синхронной машины при постоянстве синхронной ЭДС статора ()

Переменная E_Q, которая входит в уравнения для определения активной мощности , может быть переписана через переменную E_q  следующим образом:

.

Найдем выражение для определения тока . Для этого рассмотрим следующее выражение:

Выразим ток  подставляя в ранее полученное выражение уравнения, которые описывают установившийся режим работы синхронной машины (, ). В результате подстановки получим:

;

.

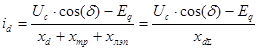Подставим полученное выражение для определения   в уравнение E_Q с учетом соотношения . В результате подстановки получим:

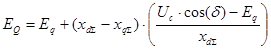
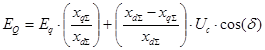
Полученное выражение определяет закон изменения ЭДС E_Q при условии постоянства синхронной ЭДС статора.

Далее преобразуем выражение для определения активной мощности  с помощью полученного выражения :

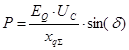
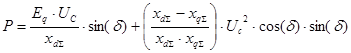
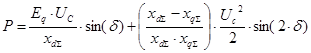
Полученное выражение носит название угловой характеристика мощности синхронной машины при постоянстве синхронной ЭДС статора.

Полученная формула показывает, что в общем случае при  характеристика мощности содержит кроме основной синусоидальной составляющей мощности также составляющую двойного угла. Амплитуда составляющей мощности двойного угла обычно не велика. Так, например, при работе машины непосредственно на шины бесконечной мощности при , , , , составляющая двойного угла равна 18% от амплитуды основной составляющей. Наличие реактивности внешней сети заметно уменьшает эту цифру: если  то указанное соотношение составляет 13%, 10% и 7,1 %.

Рассмотрим в качестве примера турбогенератор со следующими параметрами:

МВт, , кВ

, , , 

Для данной модели генератора определим зависимость электромагнитной мощности от угла δ при сопротивлении  (о.е.). В качестве базисных величин будем использовать полную мощность генератора и генераторное напряжение. Перед построением угловой характеристики мощности необходимо определить значение параметра E_q и угол δ при заданных номинальных параметров генератора.

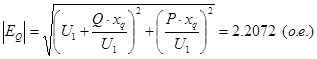
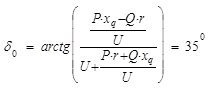
Зависимость электромагнитной мощности от угла  при имеет вид представленный на рис.4.

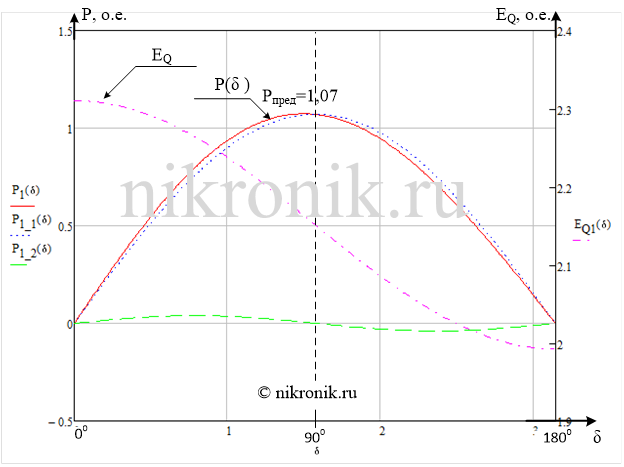
Рис.4. Угловая характеристика мощности при постоянстве синхронной ЭДС статора, а также зависимость изменения E_Q.

Как видно из рисунка, максимальная мощность соответствует углу несколько меньшему, чем 90 градусов и мало отличатся от мощности, определяемой основной синусоидальной составляющей. Поэтому при ориентировочных расчетах обычно пренебрегают влиянием неявнополюности машины.

Для данного рассматриваемого случая получили, что изменение активной мощности в диапазоне от 0 до 1,07 до 0  (о.е.), а вспомогательной ЭДС  E_Q  меняется от значения 2,31 до значения 1,99 (о.е.).

б. Угловая характеристика мощности синхронной машины при постоянстве потокосцепления контура возбуждения ()

Переменная , которая входит в уравнения для определения активной мощности , может быть переписана через переменную  следующим образом:

.

Поскольку данная формула полностью аналогична формуле записанной ранее для определения , то выражение для мощности можно записать следующее (делая соответствующие замены параметров  и  на новые  и  соответственно):

Полученное выражение определяет закон изменения ЭДС E_Q при постоянстве потокосцепления контура возбуждения..

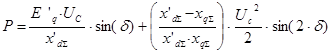
Полученное выражение носит название угловой характеристика мощности синхронной машины при постоянстве потокосцепления контура возбуждения.

Поскольку вторая составляющая выражения при углах от 0 до пи/2 отрицательна, то максимум угловой характеристики в случае  достигается при угле больше пи/2 и превышает максимальное значение мощности, отвечающее условию .

Рассмотрим в качестве примера турбогенератор со следующими параметрами (аналогично предыдущему случаю):

МВт, , кВ

, , , 

Для данной модели генератора определим зависимость электромагнитной мощности от угла δ при сопротивлении (о.е.). В качестве базисных величин будем использовать полную мощность генератора и генераторное напряжение. Перед построением угловой характеристики мощности необходимо определить значение параметра E’_q и угол δ при заданных номинальных параметров генератора.

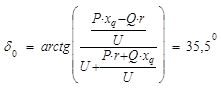
Зависимость электромагнитной мощности от угла  при имеет вид представленный на рис.5.

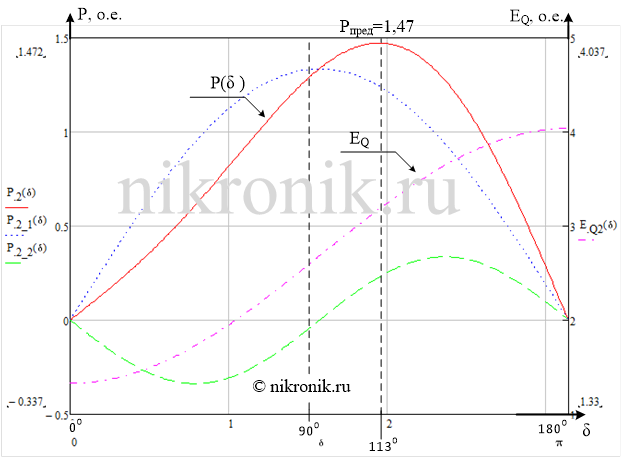
Рис.5. Угловая характеристика мощности при постоянстве потокосцепления контура возбуждения, а также зависимость изменения E_Q.

Как видно из рисунка, максимальная мощность соответствует углу большему, чем 90 градусов.

Для данного рассматриваемого случая получили, что изменение активной мощности в диапазоне от 0 до 1,47 до 0  (о.е.), а вспомогательной ЭДС  E_Q  меняется от значения 1,33 до значения 4,03 (о.е.).

в. Угловая характеристика мощности синхронной машины при постоянном напряжении на зажимах генератора ()

Для представленной ранее схемы замещения можно записать следующую систему уравнений:

П.1. Первое уравнение  из записанной системы можно переписать в следующем виде:

Полученное выражение в комплексной форме можно разложить на следующую равносильную систему уравнений:

Для того, чтобы избавиться от угла , возведем данную систему уравнений в квадрат и сложим оба уравнения:

Определим токи  и , для этого рассмотрим следующие уравнение (см. П.2).

П.2. Второе уравнение из записанной системы можно переписать в следующем виде:

В результате получим следующую систему уравнений:

Из данной системы уравнений выразим токи  и  :

П.3.Подставим полученные значения  и  в уравнение, полученное по П.1.:

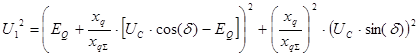
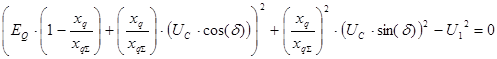
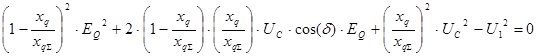
В результате преобразований получили квадратное уравнение относительно переменной E_Q. Корни квадратного уравнения  определяются по формуле:

В данном случае неизвестная E_Q определяется следующим образом:

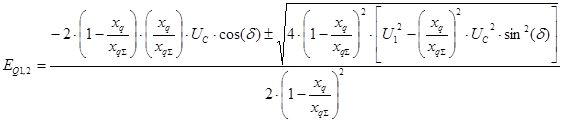
После аналитического преобразования, а также с учетом того, что физический смысл имеет только знак «+» получаем следующее выражение:

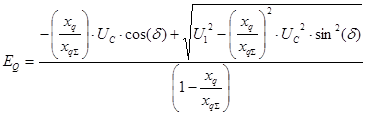
Полученное выражение дает закон изменения вспомогательной ЭДС  E_Q, необходимый для поддержания напряжения на шинах генератора .

Далее преобразуем выражение для определения активной мощности  с помощью полученного выражения E_Q:

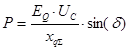
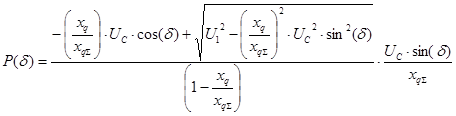
Полученное выражение носит название угловой характеристика мощности синхронной машины при постоянном напряжении на зажимах генератора.

Рассмотрим в качестве примера турбогенератор со следующими параметрами (аналогично предыдущему случаю):

МВт, , кВ

, , , 

Для данной модели генератора определим зависимость электромагнитной мощности от угла δ при сопротивлении (о.е.). В качестве базисных величин будем использовать полную мощность генератора и генераторное напряжение.

Зависимость электромагнитной мощности от угла δ при постоянном напряжении на зажимах генератора имеет вид представленный на рис.6.

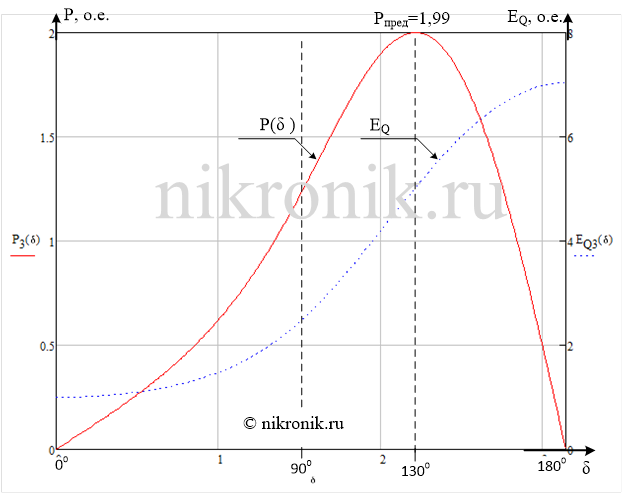
Рис.6. Угловая характеристика мощности при постоянном напряжении на зажимах генератора, а также зависимость изменения E_Q.

Как видно из рисунка, максимальная мощность соответствует углу намного большему, чем 90 градусов.

Для данного рассматриваемого случая получили, что изменение активной мощности происходит в диапазоне от 0 до 1,99 до 0  (о.е.), а вспомогательной ЭДС  E_Q  меняется от значения 1 до значения 7,04 (о.е.).

Общие выводы

Как видно из полученных расчетов, в зависимости от принятых условий, предел передаваемой мощности и угол  различен.  Следует отметить, что каждый рассмотренный случай соответствует своему типу регулирования синхронной машины:

- Постоянство синхронной ЭДС статора говорит о неизменном токе возбуждения (в установившемся режиме работы), что в свою очередь соответствует случаю отсутствия на эквивалентном генераторе автоматического регулятора возбуждения. 

- Постоянство потокосцепления контура возбуждения соответствует случаю, когда на эквивалентном генераторе установлен автоматический регулятор возбуждения пропорционального действия. 

- Постоянство напряжении на зажимах генератора обеспечивается за счет применения на эквивалентном генераторе автоматического регулятора возбуждения сильного действия. Данный регулятор (АРВ СД) отличается от АРВ ПД тем, что в закон регулирования возбуждения вводятся производные изменения параметров режима, которые обеспечивают расширение области устойчивости до еще больших значений угла δ, чем при пропорциональном регулировании.